 ώστε
ώστε  .
.1) Nα βρεθεί ο τύπος της συνάρτησης
2) Να αποδειχθεί οτι είναι

3) Να αποδειχθεί οτι η εξίσωση
 έχει μοναδική λύση
έχει μοναδική λύση4) Nα υπολογιστεί το
 με
με  κατάλληλα άκρα.
κατάλληλα άκρα.5) Nα υπολογιστεί το

6) Να υπολογιστούν τα όρια
 και
και 
Συντονιστής: R BORIS
 ώστε
ώστε  .
.
 έχει μοναδική λύση
έχει μοναδική λύση με
με  κατάλληλα άκρα.
κατάλληλα άκρα.
 και
και 
...μια αντιμετώπιση...erxmer έγραψε:Δίνεται η συνάρτησηώστε
.
1) Nα βρεθεί ο τύπος της συνάρτησης
2) Να αποδειχθεί οτι είναι
3) Να αποδειχθεί οτι η εξίσωσηέχει μοναδική λύση
4) Nα υπολογιστεί τομε
κατάλληλα άκρα.
5) Nα υπολογιστεί το
6) Να υπολογιστούν τα όριακαι
 έχουμε ισοδύναμα
έχουμε ισοδύναμα ![\int\limits_{0}^{2}{\left( f(x)\int\limits_{0}^{1}{ydy} \right)}dz=\left[ {{x}^{3}}{{t}^{3}}+3{{t}^{2}}x-t \right]_{0}^{1}\Leftrightarrow f(x)\int\limits_{0}^{1}{ydy}\int\limits_{0}^{2}{dz}={{x}^{3}}+3x-1\Leftrightarrow \int\limits_{0}^{2}{\left( f(x)\int\limits_{0}^{1}{ydy} \right)}dz=\left[ {{x}^{3}}{{t}^{3}}+3{{t}^{2}}x-t \right]_{0}^{1}\Leftrightarrow f(x)\int\limits_{0}^{1}{ydy}\int\limits_{0}^{2}{dz}={{x}^{3}}+3x-1\Leftrightarrow](/forum/ext/geomar/texintegr/latexrender/pictures/1558c55daa83efec5152f20992e971ae.png)
![f(x)\left[ \frac{{{y}^{2}}}{2} \right]_{0}^{1}\left[ z \right]_{0}^{2}={{x}^{3}}+3x-1\Leftrightarrow f(x)\cdot \frac{1}{2}\cdot 2={{x}^{3}}+3x-1\Leftrightarrow f(x)={{x}^{3}}+3x-1 f(x)\left[ \frac{{{y}^{2}}}{2} \right]_{0}^{1}\left[ z \right]_{0}^{2}={{x}^{3}}+3x-1\Leftrightarrow f(x)\cdot \frac{1}{2}\cdot 2={{x}^{3}}+3x-1\Leftrightarrow f(x)={{x}^{3}}+3x-1](/forum/ext/geomar/texintegr/latexrender/pictures/bcbfbdc8ea69b9a9e4c638459660981d.png)
 είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο  με
με  είναι γνήσια αύξουσα άρα και
είναι γνήσια αύξουσα άρα και 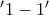 .
. οπότε για την συνάρτηση
οπότε για την συνάρτηση 
 και
και 
 οπότε υπάρχει
οπότε υπάρχει 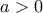 με
με  επομένως
επομένως 
 με
με  .
. είναι παραγωγίσιμη με
είναι παραγωγίσιμη με  και η
και η  αν έχει ρίζα κάποιο
αν έχει ρίζα κάποιο  τότε θα είναι είναι
τότε θα είναι είναι  (από γνωστή εφαρμογή)
(από γνωστή εφαρμογή)  που είναι άτοπο αφού
που είναι άτοπο αφού  άρα
άρα  και επειδή είναι συνεχής θα έχει σταθερό πρόσημο, και αφού
και επειδή είναι συνεχής θα έχει σταθερό πρόσημο, και αφού  είναι
είναι 
 άρα η
άρα η  γνήσια αύξουσα άρα και
γνήσια αύξουσα άρα και 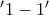 οπότε
οπότε 
 .
. για το
για το ![[a,\,\,\beta ] [a,\,\,\beta ]](/forum/ext/geomar/texintegr/latexrender/pictures/a0c13225461200d9f2405f3d7e08ab65.png) ) και με δεδομένο αυτό αν
) και με δεδομένο αυτό αν  και
και  και
και 
![\int\limits_{a}^{b}{{{f}^{-1}}}(x)dx=\int\limits_{{{f}^{-1}}(a)}^{{{f}^{-1}}(\beta )}{u{f}'(u)du}=\left[ uf(u) \right]_{{{f}^{-1}}(a)}^{{{f}^{-1}}(\beta )}-\int\limits_{{{f}^{-1}}(a)}^{{{f}^{-1}}(\beta )}{f(u)du}= \int\limits_{a}^{b}{{{f}^{-1}}}(x)dx=\int\limits_{{{f}^{-1}}(a)}^{{{f}^{-1}}(\beta )}{u{f}'(u)du}=\left[ uf(u) \right]_{{{f}^{-1}}(a)}^{{{f}^{-1}}(\beta )}-\int\limits_{{{f}^{-1}}(a)}^{{{f}^{-1}}(\beta )}{f(u)du}=](/forum/ext/geomar/texintegr/latexrender/pictures/f3e9c8f657da7c594cc50b58ad600315.png)

 με
με  και
και  και
και  και
και ![\int\limits_{-1}^{5}{{{\left( {{f}^{-1}}(x) \right)}^{10}}}dx=\int\limits_{0}^{1}{{{\left( u \right)}^{10}}}{f}'(u)du=\left[ {{u}^{10}}f(u) \right]_{0}^{1}-10\int\limits_{0}^{1}{{{u}^{9}}}f(u)du\Leftrightarrow \int\limits_{-1}^{5}{{{\left( {{f}^{-1}}(x) \right)}^{10}}}dx=\int\limits_{0}^{1}{{{\left( u \right)}^{10}}}{f}'(u)du=\left[ {{u}^{10}}f(u) \right]_{0}^{1}-10\int\limits_{0}^{1}{{{u}^{9}}}f(u)du\Leftrightarrow](/forum/ext/geomar/texintegr/latexrender/pictures/9f4cd5dda4e9a9106ed411505506bf83.png)
![\int\limits_{-1}^{5}{{{\left( {{f}^{-1}}(x) \right)}^{10}}}dx+10\int\limits_{0}^{1}{{{x}^{9}}}f(x)dx=\left[ {{u}^{10}}f(u) \right]_{0}^{1}=f(1)=3 \int\limits_{-1}^{5}{{{\left( {{f}^{-1}}(x) \right)}^{10}}}dx+10\int\limits_{0}^{1}{{{x}^{9}}}f(x)dx=\left[ {{u}^{10}}f(u) \right]_{0}^{1}=f(1)=3](/forum/ext/geomar/texintegr/latexrender/pictures/1cb3bca2423345e30aa7b3ccc9dd32bd.png)
 και
και 

 (προκύπτει άμεσα από την
(προκύπτει άμεσα από την  που έχει το σχολικό)
που έχει το σχολικό) (1)
(1) και
και 
 )
)Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες