Να δείξετε ότι για κάθε
 ισχύει :
ισχύει :
Συντονιστής: R BORIS

![\displaystyle{\int_0^1 {{x^v}{{(1 - x)}^v}dx \le \int_0^1 {\frac{1}{{{4^v}}}dx = \frac{1}{{{4^v}}}[x]\begin{array}{*{20}{c}}
1 \\
0 \\
\end{array}} } = \frac{1}{{{4^v}}} = \frac{1}{{{2^{2v}}}}} \displaystyle{\int_0^1 {{x^v}{{(1 - x)}^v}dx \le \int_0^1 {\frac{1}{{{4^v}}}dx = \frac{1}{{{4^v}}}[x]\begin{array}{*{20}{c}}
1 \\
0 \\
\end{array}} } = \frac{1}{{{4^v}}} = \frac{1}{{{2^{2v}}}}}](/forum/ext/geomar/texintegr/latexrender/pictures/0272d25655e9de9fa7ec38ad08585711.png)
 . Αυτό μπορεί να υπολογιστεί κάνοντας την αντικατάσταση
. Αυτό μπορεί να υπολογιστεί κάνοντας την αντικατάσταση  και χρησιμοποιώντας επαγωγή. Η επαγωγή δεν δουλέυει εύκολα για το
και χρησιμοποιώντας επαγωγή. Η επαγωγή δεν δουλέυει εύκολα για το

Demetres έγραψε: Το ολοκλήρωμα είναι γνωστό σαν Beta function.
Υπάρχει και μια διαφορετική απόδειξη η οποία όμως ξεφεύγει από τα σχολικά μαθηματικά. Την έβαλα σαν άσκηση εδώ.Demetres έγραψε:
Ένας άλλος τρόπος είναι ο εξής:Demetres έγραψε:Να προσθέσω ότι το ολοκλήρωμα ισούται με. Αυτό μπορεί να υπολογιστεί κάνοντας την αντικατάσταση
και χρησιμοποιώντας επαγωγή. Η επαγωγή δεν δουλέυει εύκολα για το
Η επαγωγή όμως δουλεύει μια χαρά αν προσπαθήσουμε να αποδείξουμε το πιο γενικό

 και
και  είναι
είναι ,
,  ,
, ,
, , όπου
, όπου  .
. (*)
(*)
 στο μήνυμα του Δημήτρη γίνεται
στο μήνυμα του Δημήτρη γίνεται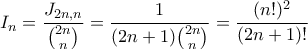


 .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες