Σας ευχαριστώ για τις απαντήσεις.
H δική μου προσέγγιση χρησιμοποιεί μόνο τον ορισμό της κοίλης συνάρτησης και για αυτό λόγω ποικιλίας την γράφω. Φυσικά επικαλύψεις με τις άλλες λύσεις είναι αναπόφευκτες.
Ας πούμε ότι τα σημεία είναι τα

και

. Αν

η

είναι η

η οποία προφανώς τέμνει την
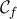
. Έστω λοιπόν ότι

οπότε η

συμπίπτει με την γραφική παράσταση της

.
Θέλουμε

για κάποιο

ή ισοδύναμα η

να έχει ρίζα. Έχουμε


αφού το

είναι κάτω από την
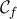
.

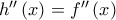
επομένως και η

είναι κοίλη. Επειδή η

είναι γνησίως φθίνουσα δεν θα είναι όλες οι τιμές της μηδέν και επομένως για κάποιο

θα είναι

.

Αν

τότε για

από το θεώρημα μεσης τιμής έχουμε
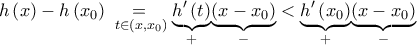
Αφού για

είναι
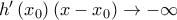
και επομένως και

. Άρα για κάποιο

είναι

και η ύπαρξη ρίζας για την

προκύπτει από το θεώρημα του Bolzano.

Αν

τότε για

επιχειρηματλογγούμε όμοια και έχουμε

και για

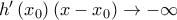
οπότε πάλι η

παίρνει αρνητική τιμή και το ζητούμενο έπεται.
Κάποια σχόλια
1) Πράγματι η βασική ιδέα είναι ότι
abgd έγραψε: ↑Δευ Μαρ 20, 2023 7:16 pm
Αν μια συνάρτηση είναι κοίλη στο τότε δεν μπορεί να είναι θετική.
κσι πράγματι μπορούμε από την εκφώνηση να απαλλαγούμε από ένα εκ των δύο σημείων.
2) Ασφαλώς αυτό που γράφει ο Γιώργος
george visvikis έγραψε: ↑Δευ Μαρ 20, 2023 2:30 pm
Φέρνω μία εφαπτομένη

της

που να μην είναι παράλληλη στην

Τότε η

τέμνει την

Αν το σημείο τομής τους είναι το σημείο επαφής, τότε τελειώσαμε. Αν όμως οι ευθείες τέμνονται σε κάποιο άλλο σημείο, έστω

τότε αυτό το σημείο θα βρίσκεται πάνω από την

(αφού είναι κοίλη). Άρα η ευθεία

έχει τα σημεία

κάτω από την καμπύλη και ένα τουλάχιστον σημείο της πάνω από αυτήν. Επομένως η

τέμνει την
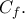
είναι τεκμηριωμένο αφού με μια-δύο επεμβάσεις μπορεί η γεωμετρική γλώσσα να μεταφραστεί σε "σχολική αναλυτική". Αυτά επί της μαθηματικής ουσίας. Στις εξετάσεις όμως τα πράγματα είναι διαφορετικά. Όσες φορές (λίγες) έχω δει σε κάποιο γραπτό τέτοιου είδους επιχειρηματολογία την έχω χαρεί. Ωστόσο έχω διαπιστώσει ότι οι βαθμολογητές τρέφουν κάποιου είδους δυδανεξία στα γεωμετρικά επιχειρήματα και απαιτούν ακόμη και για απλές καταστάσεις "αναλυτικές" αιτιολογήσεις.
 ορισμένη στους πραγματικούς και δύο διάφορα σημεία
ορισμένη στους πραγματικούς και δύο διάφορα σημεία  ,
,  κάτω από την γραφική της παράσταση
κάτω από την γραφική της παράσταση 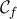 . Να αποδειχθεί ότι η ευθεία
. Να αποδειχθεί ότι η ευθεία  τέμνει την
τέμνει την 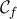 .
.
 . Αν
. Αν  , το ζητούμενο είναι προφανές. Ας είναι λοιπόν
, το ζητούμενο είναι προφανές. Ας είναι λοιπόν  και ας είναι
και ας είναι 

 , οπότε αποκλείεται να ισχύει
, οπότε αποκλείεται να ισχύει 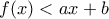 για κάθε
για κάθε 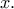
 για κάθε
για κάθε  . Από το κοίλο της
. Από το κοίλο της  θα ισχύει επίσης
θα ισχύει επίσης  και
και  για κάθε
για κάθε  , άτοπο αφού η
, άτοπο αφού η  είναι γνησίως φθίνουσα.
είναι γνησίως φθίνουσα.

 της
της  που να μην είναι παράλληλη στην
που να μην είναι παράλληλη στην  Τότε η
Τότε η  τότε αυτό το σημείο θα βρίσκεται πάνω από την
τότε αυτό το σημείο θα βρίσκεται πάνω από την  κάτω από την καμπύλη και ένα τουλάχιστον σημείο της πάνω από αυτήν. Επομένως η
κάτω από την καμπύλη και ένα τουλάχιστον σημείο της πάνω από αυτήν. Επομένως η 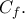
 τότε δεν μπορεί να είναι θετική.
τότε δεν μπορεί να είναι θετική. τέτοιο ώστε:
τέτοιο ώστε:
 τότε, εφόσον
τότε, εφόσον  , θα είναι:
, θα είναι: 
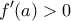 τότε, εφόσον
τότε, εφόσον 

 οποιαδήποτε ευθεία που περνάει από το
οποιαδήποτε ευθεία που περνάει από το 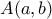 , το οποίο είναι κάτω από την γραφική παράσταση της
, το οποίο είναι κάτω από την γραφική παράσταση της 
 είναι κοίλη θα έχει και αρνητικές τιμές.
είναι κοίλη θα έχει και αρνητικές τιμές.  μία αρνητική τιμή, τότε από θεώρημα Bolzano μεταξύ των
μία αρνητική τιμή, τότε από θεώρημα Bolzano μεταξύ των  η
η  .
. βρίσκεται κάτω από την γραφική παράσταση μιας κοίλης συνάρτησης τότε οποιαδήποτε ευθεία, η οποία διέρχεται από το
βρίσκεται κάτω από την γραφική παράσταση μιας κοίλης συνάρτησης τότε οποιαδήποτε ευθεία, η οποία διέρχεται από το 

 της
της  Αν η ΑΒ βρισκεται πανω από την
Αν η ΑΒ βρισκεται πανω από την  γιατι αυτή βρίσκεται κατω από την
γιατι αυτή βρίσκεται κατω από την  τότε τα σημεία
τότε τα σημεία  συνευθειακά
συνευθειακά ή
ή 
 να ανήκει στο σύνολο τιμων της
να ανήκει στο σύνολο τιμων της  είναι το
είναι το ![\displaystyle{(-\infty,M]} \displaystyle{(-\infty,M]}](/forum/ext/geomar/texintegr/latexrender/pictures/11b3e69293e36216027e73ce2ffba503.png) ή το
ή το  γιατι οποιοσδήποτε αριθμός <Μ είναι στοΙχείο του συνόλου τιμών κι ετσι
γιατι οποιοσδήποτε αριθμός <Μ είναι στοΙχείο του συνόλου τιμών κι ετσι  οποτε η ΑΒ τεμνει την
οποτε η ΑΒ τεμνει την  και
και  . Αν
. Αν  η
η  η οποία προφανώς τέμνει την
η οποία προφανώς τέμνει την  οπότε η
οπότε η  .
. για κάποιο
για κάποιο  ή ισοδύναμα η
ή ισοδύναμα η  να έχει ρίζα. Έχουμε
να έχει ρίζα. Έχουμε
 αφού το
αφού το 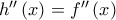 επομένως και η
επομένως και η  είναι κοίλη. Επειδή η
είναι κοίλη. Επειδή η  είναι γνησίως φθίνουσα δεν θα είναι όλες οι τιμές της μηδέν και επομένως για κάποιο
είναι γνησίως φθίνουσα δεν θα είναι όλες οι τιμές της μηδέν και επομένως για κάποιο  θα είναι
θα είναι  .
. Αν
Αν  τότε για
τότε για  από το θεώρημα μεσης τιμής έχουμε
από το θεώρημα μεσης τιμής έχουμε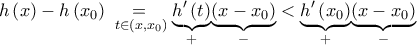
 είναι
είναι 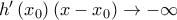 και επομένως και
και επομένως και  . Άρα για κάποιο
. Άρα για κάποιο  είναι
είναι  και η ύπαρξη ρίζας για την
και η ύπαρξη ρίζας για την  τότε για
τότε για  επιχειρηματλογγούμε όμοια και έχουμε
επιχειρηματλογγούμε όμοια και έχουμε
