Θα ήθλεα τη βόηθειά σας στο παρακάτω, καθώς δεν μπορώ να βρω τι μου διαφεύγει.
Για συνάρτηση
![f:\left [ 0, +\infty \right ]\rightarrow \mathbb{R} f:\left [ 0, +\infty \right ]\rightarrow \mathbb{R}](/forum/ext/geomar/texintegr/latexrender/pictures/e874b1990603c3253a69c922ea44f9ec.png) παραγωγίσιμη και κοίλη, με
παραγωγίσιμη και κοίλη, με  (και
(και  ), μπορούμε να συμπεράνουμε ότι
), μπορούμε να συμπεράνουμε ότι  για
για  ;
;Σύμφωνα με το σχολικό, η
 είναι γνησίως φθίνουσα στο εσωτερικό του διαστήματος. Πώς μπορούμε να ξεπεράσουμε το εμπόδιο και να συγκρίνουμε με το
είναι γνησίως φθίνουσα στο εσωτερικό του διαστήματος. Πώς μπορούμε να ξεπεράσουμε το εμπόδιο και να συγκρίνουμε με το  ;
;Ευχαριστώ πολύ!
Update Επειδή τώρα κατάλαβα πώς μπορώ να ανεβάσω φωτο, επισυνάπτω την άσκηση-εμπνευση της απορίας.
Και πάλι ευχαριστώ.

 τότε,
τότε,  , θα είναι:
, θα είναι: 
 γιατί τότε
γιατί τότε  .
. 
 !!!
!!! )" ,
)" , 

 είναι παραγωγίσιμη με
είναι παραγωγίσιμη με  και κοίλη τότε:
και κοίλη τότε:
![\displaystyle{f\left([a,+\infty)\right)=\left(-\infty,f(a)\right]} \displaystyle{f\left([a,+\infty)\right)=\left(-\infty,f(a)\right]}](/forum/ext/geomar/texintegr/latexrender/pictures/97512b8fc73ac31badce6b9773647b2b.png)
 είναι κοίλη, η γραφική της παράσταση είναι πιο κάτω από την εφαπτομένη της στο σημείο
είναι κοίλη, η γραφική της παράσταση είναι πιο κάτω από την εφαπτομένη της στο σημείο 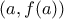 :
: , με την ισότητα να ισχύει μόνο για
, με την ισότητα να ισχύει μόνο για  .
. τέτοιο ώστε
τέτοιο ώστε  .
. είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο  θα είναι
θα είναι 
![\displaystyle{[a,k]} \displaystyle{[a,k]}](/forum/ext/geomar/texintegr/latexrender/pictures/243ecc35e5805fa87b7b6ea96a508788.png) και θα ισχύει:
και θα ισχύει:![\displaystyle{f(x)\geq f(a), \ \ \forall x\in [a,k]} \displaystyle{f(x)\geq f(a), \ \ \forall x\in [a,k]}](/forum/ext/geomar/texintegr/latexrender/pictures/187e27bc1caf45613b178724b5943491.png) και, από την
και, από την  θα έχουμε:
θα έχουμε: ![\displaystyle{f(x)=f(a), \ \ \forall x\in [a,k]} \displaystyle{f(x)=f(a), \ \ \forall x\in [a,k]}](/forum/ext/geomar/texintegr/latexrender/pictures/c9a28c3905cf6a3c2da56b5d1b56a510.png)
![\displaystyle{f'(x)=0, \ \ \forall x\in [a,k]} \displaystyle{f'(x)=0, \ \ \forall x\in [a,k]}](/forum/ext/geomar/texintegr/latexrender/pictures/678d494c5354d00c562265d4d9a2c2bf.png) , δηλαδή η
, δηλαδή η ![\displaystyle{ [a,k]} \displaystyle{ [a,k]}](/forum/ext/geomar/texintegr/latexrender/pictures/bddec05e181a0308c3091b972a15d643.png) το οποίο είναι άτοπο.
το οποίο είναι άτοπο. οπότε
οπότε ![\displaystyle{f\left([a,+\infty)\right)=\left(\lim_{x\to +\infty}f(x),f(a)\right]} \displaystyle{f\left([a,+\infty)\right)=\left(\lim_{x\to +\infty}f(x),f(a)\right]}](/forum/ext/geomar/texintegr/latexrender/pictures/34f8f98d82811db264a7c1d5791479f3.png)
 είναι:
είναι:  .
.  και έτσι
και έτσι 
 οπότε
οπότε  παραγωγίσιμη, κοίλη με
παραγωγίσιμη, κοίλη με 
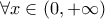 ισχύουν:
ισχύουν:

 η αρχική της
η αρχική της  , θεωρούμε τη συνάρτηση
, θεωρούμε τη συνάρτηση  με
με 
 είναι συνεχής στο
είναι συνεχής στο 
