
Δεκτή οποιαδήποτε λύση
Συντονιστής: KAKABASBASILEIOS
Καλημέρα Γιώργη!
 Είναι
Είναι  και η εφαπτομένη της
και η εφαπτομένη της  στο
στο  έχει εξίσωση
έχει εξίσωση 
 για κάθε
για κάθε  που σημαίνει ότι η
που σημαίνει ότι η  βρίσκεται πάνω από την
βρίσκεται πάνω από την  (εξαιρουμένου του σημείου επαφής), άρα
(εξαιρουμένου του σημείου επαφής), άρα 
 για
για  με
με (η πρώτη παρένθεση
(η πρώτη παρένθεση ενώ η δεύτερη αρνητική στο πεδίο ορισμού της). Άρα η
ενώ η δεύτερη αρνητική στο πεδίο ορισμού της). Άρα η  παρουσιάζει ελάχιστο στο
παρουσιάζει ελάχιστο στο  και το ζητούμενο έπεται.
και το ζητούμενο έπεται. είναι η διάμεσος του τραπεζίου και το
είναι η διάμεσος του τραπεζίου και το  είναι εφαπτόμενο τμήμα , οπότε
είναι εφαπτόμενο τμήμα , οπότε  .
. ισχύει ως ισότητα .‘Εστω ότι
ισχύει ως ισότητα .‘Εστω ότι  . Τότε :
. Τότε :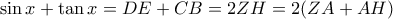




 ,
,
 , αρκεί
, αρκεί 




 (αποδεικνύεται εύκολα)
(αποδεικνύεται εύκολα)


 απ' όπου
απ' όπου 

 και
και  προκύπτει η αποδεικτέα σχέση
προκύπτει η αποδεικτέα σχέση  .
. , το
, το  , είναι πιο κοντά στο
, είναι πιο κοντά στο  , απ' ότι η
, απ' ότι η  .
. . Στην πραγματικότητα ισχύει κάτι πολύ ισχυρότερο , δηλαδή :
. Στην πραγματικότητα ισχύει κάτι πολύ ισχυρότερο , δηλαδή :  . Αυτό είναι άσκηση (
. Αυτό είναι άσκηση (  , σελ.
, σελ.  ) του σχολικού βιβλίου .
) του σχολικού βιβλίου .Ας δούμε και μία ανορθόδοξη αλλά απλή μέθοδο την οποία δεν έχω δει πουθενά αλλά η οποία λειτουργεί άριστα σε ακρότατα συναρτήσεων που δίνονται ως πηλίκα. Είχα πολλές φορές αφορμή να την χρησιμοποιήσω στο φόρουμ αλλά δεν βρήκα την ευκαιρία.
 συνεχείς στο
συνεχείς στο ![[a,\,b] [a,\,b]](/forum/ext/geomar/texintegr/latexrender/pictures/d2524b9940ce1c636bfb26ae09a941d2.png) και παραγωγίσιμες στο
και παραγωγίσιμες στο  με πουθενά μηδενιζόμενο
με πουθενά μηδενιζόμενο  , έχουμε για κάποιο
, έχουμε για κάποιο 

 , και
, και  έχουμε
έχουμε  .
.  . Yπάρχουν πολλοί τρόποι να το δούμε. Π.χ. ένας χωρίς παραγώγους είναι
. Yπάρχουν πολλοί τρόποι να το δούμε. Π.χ. ένας χωρίς παραγώγους είναι  (διότι
(διότι  καθώς η συνάρτηση είναι φθίνουσα).
καθώς η συνάρτηση είναι φθίνουσα).Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 10 επισκέπτες