 , έχει αρχή το κέντρο του τεταρτοκυκλίου
, έχει αρχή το κέντρο του τεταρτοκυκλίου  , ακτίνας
, ακτίνας  και τέμνει το τόξο .
και τέμνει το τόξο .Φέρουμε τμήμα :
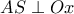 . Υπολογίστε το μέγιστο εμβαδόν του τετραπλεύρου
. Υπολογίστε το μέγιστο εμβαδόν του τετραπλεύρου  .
.Συντονιστής: KAKABASBASILEIOS
 , έχει αρχή το κέντρο του τεταρτοκυκλίου
, έχει αρχή το κέντρο του τεταρτοκυκλίου  , ακτίνας
, ακτίνας  και τέμνει το τόξο .
και τέμνει το τόξο .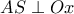 . Υπολογίστε το μέγιστο εμβαδόν του τετραπλεύρου
. Υπολογίστε το μέγιστο εμβαδόν του τετραπλεύρου  .
.Τα τρίγωνα
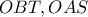 είναι ίσα ,γιατί είναι ορθογωνια και
είναι ίσα ,γιατί είναι ορθογωνια και 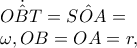 Αρα θέτω
Αρα θέτω 
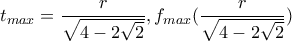
Έστω
 . Είναι προφανώς
. Είναι προφανώς 
 .
. 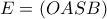 , είναι το άθροισμα των εμβαδών των τριγώνων ,
, είναι το άθροισμα των εμβαδών των τριγώνων ,  .
. και αφού
και αφού  η προηγούμενη γίνεται:
η προηγούμενη γίνεται: 
 .
. 
 δίδει :
δίδει :  και άρα
και άρα  .
.  το ίσον ισχύει όταν
το ίσον ισχύει όταν 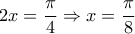 .
.Έστω



 απ' όπου βρίσκω ότι για
απ' όπου βρίσκω ότι για 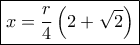

 η τομή της
η τομή της  με τον κύκλο
με τον κύκλο  . Καθώς η
. Καθώς η  διαγράφει τον κύκλο
διαγράφει τον κύκλο  και το
και το  άρα
άρα το
το  θα διαγράψει τον κύκλο
θα διαγράψει τον κύκλο 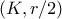 . Επειδή τώρα
. Επειδή τώρα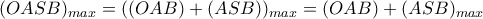
 προφανώς επιτυγχάνεται όταν μεγιστοποιείται το
προφανώς επιτυγχάνεται όταν μεγιστοποιείται το  δηλαδή όταν
δηλαδή όταν  .
.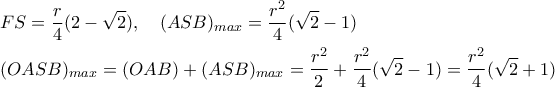
nickchalkida έγραψε: ↑Σάβ Νοέμ 27, 2021 11:21 pmΔίνω και μια γεωμετρική προσέγγιση ... που ίσως δεν άπτεται του φακέλου ... αλλά νομίζω ωφελεί.
Έστωη τομή της
με τον κύκλο
. Καθώς η
διαγράφει τον κύκλο
και το
άρα
θα διαγράψει τον ίδιο κύκλο, και επειδήτο
θα διαγράψει τον κύκλο
. Επειδή τώρα
τοπροφανώς επιτυγχάνεται όταν μεγιστοποιείται το
δηλαδή όταν
.
Εύκολα τότε βρίσκω για αυτή την θέση
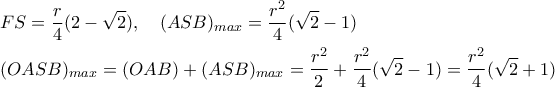
Θεωρούμε τον περίκυκλο του τριγώνου
 τον οποίο η κάθετος από το
τον οποίο η κάθετος από το  στην
στην τέμνει στο
τέμνει στο  οπότε,το
οπότε,το  είναι ορθογώνιο
είναι ορθογώνιο άρα
άρα  κι επειδή
κι επειδή  αρκεί να γίνει μέγιστο το
αρκεί να γίνει μέγιστο το 
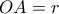 είναι σταθερή,συνεπώς αρκεί το ύψος
είναι σταθερή,συνεπώς αρκεί το ύψος  να γίνει μέγιστο ,που
να γίνει μέγιστο ,που είναι μέσον του τόξου
είναι μέσον του τόξου 
 κι εύκολα
κι εύκολα 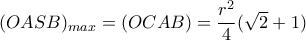
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 11 επισκέπτες