 όπου
όπου  .
.- Να μελετηθεί ως προς τη μονοτονία η
 .
. - Αν
 οι ρίζες της
οι ρίζες της  τότε να υπολογιστεί το όριο:
τότε να υπολογιστεί το όριο:

Συντονιστής: KAKABASBASILEIOS
 όπου
όπου  .
. .
. οι ρίζες της
οι ρίζες της  τότε να υπολογιστεί το όριο:
τότε να υπολογιστεί το όριο:

Καλησπέρα. Μια προσπάθεια μετά από πολύ καιρό ...Tolaso J Kos έγραψε: ↑Δευ Ιούλ 26, 2021 11:39 amΔίδεται η συνάρτησηόπου
.
- Να μελετηθεί ως προς τη μονοτονία η
.
- Αν
οι ρίζες της
τότε να υπολογιστεί το όριο:
 έχει πεδίο ορισμού το
έχει πεδίο ορισμού το  και είναι παραγωγίσιμη με
και είναι παραγωγίσιμη με  .
. . Διακρίνουμε περιπτώσεις :
. Διακρίνουμε περιπτώσεις : . Το τριώνυμο έχει
. Το τριώνυμο έχει  και
και  οπότε έχει δύο ρίζες τις:
οπότε έχει δύο ρίζες τις: και
και  .
. , οπότε και το πρόσημο του τριωνύμου είναι ίδιο με το πρόσημο της διακρίνουσας.
, οπότε και το πρόσημο του τριωνύμου είναι ίδιο με το πρόσημο της διακρίνουσας.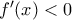 άρα και
άρα και  :γνησίως φθίνουσα στο
:γνησίως φθίνουσα στο ![(-\infty ,\beta ] (-\infty ,\beta ]](/forum/ext/geomar/texintegr/latexrender/pictures/7955154fcbe7a814f41af14fb38ad4f6.png)
 άρα και
άρα και  :γνησίως αύξουσα στο
:γνησίως αύξουσα στο ![[\beta,\alpha ] [\beta,\alpha ]](/forum/ext/geomar/texintegr/latexrender/pictures/c42351ce47998aee592bb63f39e20ac6.png)

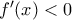 άρα και
άρα και  :γνησίως φθίνουσα στο
:γνησίως φθίνουσα στο 
 . Το τριώνυμο έχει
. Το τριώνυμο έχει  και
και  . Τώρα έχουμε :
. Τώρα έχουμε : άρα και
άρα και  :γνησίως αύξουσα στο
:γνησίως αύξουσα στο ![(-\infty ,\alpha ] (-\infty ,\alpha ]](/forum/ext/geomar/texintegr/latexrender/pictures/dc47c095b9938f15d0cfc4ab3cc84c12.png)
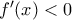 άρα και
άρα και  :γνησίως φθίνουσα στο
:γνησίως φθίνουσα στο ![[\alpha , \beta ] [\alpha , \beta ]](/forum/ext/geomar/texintegr/latexrender/pictures/ae4a46da42598349ebcbafbd53e02a2c.png)
 άρα και
άρα και  :γνησίως αύξουσα στο
:γνησίως αύξουσα στο 
 . Είναι
. Είναι  και επειδή η
και επειδή η  : συνεχής είναι γνησίως φθίνουσα στο
: συνεχής είναι γνησίως φθίνουσα στο  .
. . Είναι
. Είναι  και επειδή η
και επειδή η  : συνεχής είναι γνησίως αύξουσα στο
: συνεχής είναι γνησίως αύξουσα στο  .
. . Το τριώνυμο έχει
. Το τριώνυμο έχει  και
και  οπότε
οπότε 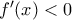 άρα και
άρα και  :γνησίως φθίνουσα στο
:γνησίως φθίνουσα στο 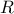 .
. . Το τριώνυμο έχει
. Το τριώνυμο έχει  και
και  οπότε
οπότε  άρα και
άρα και  :γνησίως αύξουσα στο
:γνησίως αύξουσα στο 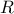 .
. ,
, 
 . Ξαναθέτω
. Ξαναθέτω 

 .
. οπότε από κανόνα de l' Hospital έχουμε:
οπότε από κανόνα de l' Hospital έχουμε: 
 .
.
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες