 όπου
όπου  τρίγωνο με το μέγιστο εμβαδόν.
τρίγωνο με το μέγιστο εμβαδόν.Συντονιστής: KAKABASBASILEIOS
 όπου
όπου  τρίγωνο με το μέγιστο εμβαδόν.
τρίγωνο με το μέγιστο εμβαδόν.
 . Δυστυχώς έχασα τη λύση.
. Δυστυχώς έχασα τη λύση.
 η έλλειψη και ας είναι
η έλλειψη και ας είναι  τρία σημεία αυτής.
τρία σημεία αυτής.
 .
. τότε
τότε 

 τρίγωνο μεγίστου εμβαδού εγγεγραμμένο στην έλλειψη
τρίγωνο μεγίστου εμβαδού εγγεγραμμένο στην έλλειψη  με
με  Είναι φανερό ότι η
Είναι φανερό ότι η  οφείλει να είναι παράλληλη προς την εφαπτομένη στο
οφείλει να είναι παράλληλη προς την εφαπτομένη στο  άρα αν
άρα αν  είναι η εξίσωση της
είναι η εξίσωση της  ισχύει η
ισχύει η  Θα δείξουμε ότι για κάθε
Θα δείξουμε ότι για κάθε  προκύπτει ένα τρίγωνο μεγίστου εμβαδού με
προκύπτει ένα τρίγωνο μεγίστου εμβαδού με 
 του τυχόντος εγγεγραμμένου τριγώνου
του τυχόντος εγγεγραμμένου τριγώνου  ισχύει βεβαίως η
ισχύει βεβαίως η  όπου
όπου  η απόσταση του
η απόσταση του  από την
από την  Θα εκφράσουμε το
Θα εκφράσουμε το  ως συνάρτηση του
ως συνάρτηση του  και θα επιδιώξουμε την μεγιστοποίηση της.
και θα επιδιώξουμε την μεγιστοποίηση της. παρατηρούμε ότι
παρατηρούμε ότι  όπου τα
όπου τα  είναι ρίζες της δευτεροβάθμιας
είναι ρίζες της δευτεροβάθμιας  οπότε
οπότε  και
και  προκύπτει από όλα αυτά η
προκύπτει από όλα αυτά η 
 παρατηρούμε ότι από τις
παρατηρούμε ότι από τις  και
και  προκύπτουν (αβλαβώς υποθέτοντας
προκύπτουν (αβλαβώς υποθέτοντας  ) οι
) οι  και
και  και τελικά η
και τελικά η 
 Ο μηδενισμός της
Ο μηδενισμός της  είναι ισοδύναμος προς την
είναι ισοδύναμος προς την  που συνεπάγεται μεγιστοποίηση για
που συνεπάγεται μεγιστοποίηση για 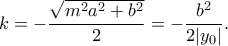
 ότι δηλαδή για κάθε σημείο
ότι δηλαδή για κάθε σημείο  επί της έλλειψης υπάρχει μεγίστου εμβαδού
επί της έλλειψης υπάρχει μεγίστου εμβαδού  εγγεγραμμένο τρίγωνο
εγγεγραμμένο τρίγωνο  ... επαληθεύοντας την ήδη επισημανθείσα (εδώ) γεωμετρική/προβολική φύση του προβλήματος.
... επαληθεύοντας την ήδη επισημανθείσα (εδώ) γεωμετρική/προβολική φύση του προβλήματος.Με τον μετασχηματισμόTolaso J Kos έγραψε: ↑Τετ Ιούλ 07, 2021 4:36 pmΝα εγγράψετε σε δοθείσα έλλειψηόπου
τρίγωνο με το μέγιστο εμβαδόν.
 η έλλειψη γίνεται κύκλος με ακτίνα
η έλλειψη γίνεται κύκλος με ακτίνα 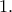
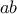 και το
και το

 στον κύκλο
στον κύκλο  αντιστοιχώντας το σημείο
αντιστοιχώντας το σημείο  στο σημείο
στο σημείο  .
. τρία διαφορετικά σημεία της έλλειψης και
τρία διαφορετικά σημεία της έλλειψης και  οι "προβολές" τους στον μοναδιαίο κύκλο, ισχύει:
οι "προβολές" τους στον μοναδιαίο κύκλο, ισχύει: ,
,  το εγγεγραμμένο ισόπλευρο τρίγωνο στον μοναδιαίο κύκλο, για το οποίο θεωρούμε γνωστό ότι έχει το μέγιστο εμβαδό.
το εγγεγραμμένο ισόπλευρο τρίγωνο στον μοναδιαίο κύκλο, για το οποίο θεωρούμε γνωστό ότι έχει το μέγιστο εμβαδό. της έλλειψης στο
της έλλειψης στο  του κύκλου.
του κύκλου. και βρίσκουμε τα σημεία
και βρίσκουμε τα σημεία  της έλλειψης που οι "προβολές" τους στον κύκλο είναι τα
της έλλειψης που οι "προβολές" τους στον κύκλο είναι τα  .
. είναι το ζητούμενο τρίγωνο.
είναι το ζητούμενο τρίγωνο.

Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 7 επισκέπτες