 , τριγώνου
, τριγώνου  είναι οι τομές των ευθειών
είναι οι τομές των ευθειών  και
και  ( η "βόρεια" ) ,
( η "βόρεια" ) ,με τον κύκλο
 . Υπολογίστε το μέγιστο εμβαδόν αυτού του τριγώνου . ( Φυσικά :
. Υπολογίστε το μέγιστο εμβαδόν αυτού του τριγώνου . ( Φυσικά :  ) .
) .Συντονιστής: KAKABASBASILEIOS
 , τριγώνου
, τριγώνου  είναι οι τομές των ευθειών
είναι οι τομές των ευθειών  και
και  ( η "βόρεια" ) ,
( η "βόρεια" ) , . Υπολογίστε το μέγιστο εμβαδόν αυτού του τριγώνου . ( Φυσικά :
. Υπολογίστε το μέγιστο εμβαδόν αυτού του τριγώνου . ( Φυσικά :  ) .
) . είναι η
είναι η  .
. ![\displaystyle{\begin{tikzpicture}
\draw (0, 0) circle(4cm);
\draw[dashed] (-4.6, -2) -- (4.4, -2);
\draw[dashed] (-2, -4) -- (-2, 4);
\draw[fill=black] (0, 0) circle(2pt);
\draw[line width=1.6pt, cyan] (-3.46, -2) -- (-2, 3.46) -- (3.46, -2) -- cycle;
\draw (-2, 3.46) node[above left]{A};
\draw (-3.46, -2) node[below left]{B};
\draw (3.46, -2) node[below right]{\text{\gr Γ}};
\draw (0, 0) node[below]{O};
\end{tikzpicture}} \displaystyle{\begin{tikzpicture}
\draw (0, 0) circle(4cm);
\draw[dashed] (-4.6, -2) -- (4.4, -2);
\draw[dashed] (-2, -4) -- (-2, 4);
\draw[fill=black] (0, 0) circle(2pt);
\draw[line width=1.6pt, cyan] (-3.46, -2) -- (-2, 3.46) -- (3.46, -2) -- cycle;
\draw (-2, 3.46) node[above left]{A};
\draw (-3.46, -2) node[below left]{B};
\draw (3.46, -2) node[below right]{\text{\gr Γ}};
\draw (0, 0) node[below]{O};
\end{tikzpicture}}](/forum/ext/geomar/texintegr/latexrender/pictures/2b35fd7c6d6a7b0f09ed3624a0867ae0.png)
 τέμνει τον κύκλο στα σημεία
τέμνει τον κύκλο στα σημεία  και
και  . Τέλος, το "βόρειο" σημείο στο οποίο τέμνει η ευθεία
. Τέλος, το "βόρειο" σημείο στο οποίο τέμνει η ευθεία  τον κύκλο είναι το
τον κύκλο είναι το  . Απλοί υπολογισμοί δείχνουν ότι
. Απλοί υπολογισμοί δείχνουν ότι  ,
,  και
και  . Ο Ήρωνας μας λέει ότι
. Ο Ήρωνας μας λέει ότι
 . Η μέγιστη τιμή τότε είναι
. Η μέγιστη τιμή τότε είναι  .
. . Αφήνω την λύση ως κεντρική ιδέα της λύσης μου.
. Αφήνω την λύση ως κεντρική ιδέα της λύσης μου.
 τα σημεία που οι ευθείες
τα σημεία που οι ευθείες  τέμνουν του άξονες .
τέμνουν του άξονες .  είναι το ύψος του
είναι το ύψος του  και
και  το σημείο που η ευθεία
το σημείο που η ευθεία 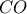 τέμνει την
τέμνει την 
 έχουν κάθετες πλευρές,
έχουν κάθετες πλευρές, ίσες και τις υποτείνουσες άρα είναι ίσα
ίσες και τις υποτείνουσες άρα είναι ίσα 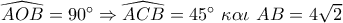 .
. το μέγιστο εμβαδόν
το μέγιστο εμβαδόν  θα το πιάσουμε όταν
θα το πιάσουμε όταν  και
και 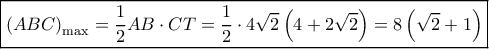
 τότε είναι ισοσκελές με κορυφή το
τότε είναι ισοσκελές με κορυφή το  .
. από τις γενικές του διαφορικού λογισμού του σχολικού βιβλίου )
από τις γενικές του διαφορικού λογισμού του σχολικού βιβλίου ) ( βέβαια το
( βέβαια το  πρέπει να γίνει
πρέπει να γίνει 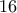 ) .
) .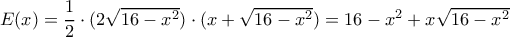 κ.λ.π.
κ.λ.π. είναι η ευθεία
είναι η ευθεία  . Επειδή το
. Επειδή το  είναι ορθογώνιο ισοσκελές
είναι ορθογώνιο ισοσκελές 
 είναι σταθερό και ίσο με
είναι σταθερό και ίσο με  .
.  μεγιστοποιείται όταν το
μεγιστοποιείται όταν το  μεγιστοποιείται, που συμβαίνει όταν η
μεγιστοποιείται, που συμβαίνει όταν η  συμπέσει
συμπέσει και είναι τότε
και είναι τότε 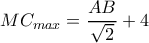 , (το
, (το  είναι κορυφή κανονικού 16γώνου). Τότε λοιπόν
είναι κορυφή κανονικού 16γώνου). Τότε λοιπόν
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης