 ορισμένη σε ένα διάστημα
ορισμένη σε ένα διάστημα  και
και  . Υποθέτουμε ότι το όριο
. Υποθέτουμε ότι το όριο
υπάρχει και είναι πραγματικός αριθμός. Ο αριθμός αυτός ονομάζεται παράγωγος Riemann της
 στο
στο  .
.- Να δειχθεί ότι αν η
 είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο  τότε υπάρχει η παράγωγος Riemann στο
τότε υπάρχει η παράγωγος Riemann στο  και ισχύει
και ισχύει  .
. - Θεωρούμε τη συνάρτηση
 . Να δειχθεί ότι ενώ η
. Να δειχθεί ότι ενώ η  δεν είναι παραγωγίσιμη στο
δεν είναι παραγωγίσιμη στο  εντούτοις υπάρχει η παράγωγος Riemann στο
εντούτοις υπάρχει η παράγωγος Riemann στο  .
.


 και παίρνοντας όριο
και παίρνοντας όριο 
 έχουμε για την παραπάνω παράσταση ότι
έχουμε για την παραπάνω παράσταση ότι  , και λοιπά. Εδώ
, και λοιπά. Εδώ 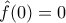 .
.