KARKAR έγραψε: ↑Τρί Ιαν 26, 2021 7:54 pm
Α) Βρείτε την μέγιστη τιμή της συνάρτησης :

Η ακτίνα του εγκύκλου.pngΒ) Το ισοσκελές τρίγωνο

, έχει σταθερή βάση :

και μεταβλητό ύψος :

.
Βα) Να εκφράσετε την ακτίνα

του εγκύκλου

του τριγώνου , συναρτήσει του ύψους

.
Ββ) Δείξτε ότι η συνάρτηση του Βα) είναι γνησίως αύξουσα και κυρτή . Δώστε και σχήμα της
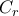
.
Για το A) δεν χρειάζεται παραγώγιση (το λέω επειδή η άσκηση είναι στον φάκελο του Διαφορικού Λογισμού, βλέπε όμως παρακάτω) αλλά βγαίνει απλά: Θέτουμε

, οπότε
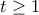
και η παράσταση είναι η
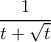
. Ο παρονομαστής ως γνήσια αύξουσα συνάρτηση (είναι άθροισμα από δύο τέτοιες) έχει ελάχιστη τιμή στο

(δηλαδή την μικρότερη επιτρεπτή τιμή του

). Άρα η δοθείσα έχει μέγιστη τιμή
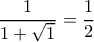
.
Β) Φέρνουμε την κάθετο

στην πλευρά

, δηλαδή ουσιαστικά ενώνουμε το

με το σημείο επαφής. Τότε τα ορθογώνια τρίγωνα

είναι όμοια και άρα

ή αλλιώς
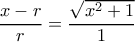
. Έπεται

Έχει παράγωγο (εδώ φαίνεται γιατί η άσκηση είναι τελικά στον σωστό φάκελο) την παραπάνω

, οπότε το Ββ) άμεσο. Το σχήμα της είναι σαν το άνω μισό ενός

, με όριο

(άμεσο) καθώς


 , έχει σταθερή βάση :
, έχει σταθερή βάση :  και μεταβλητό ύψος :
και μεταβλητό ύψος :  .
. του εγκύκλου
του εγκύκλου  του τριγώνου , συναρτήσει του ύψους
του τριγώνου , συναρτήσει του ύψους  .
. .
.
 , οπότε
, οπότε 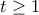 και η παράσταση είναι η
και η παράσταση είναι η 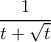 . Ο παρονομαστής ως γνήσια αύξουσα συνάρτηση (είναι άθροισμα από δύο τέτοιες) έχει ελάχιστη τιμή στο
. Ο παρονομαστής ως γνήσια αύξουσα συνάρτηση (είναι άθροισμα από δύο τέτοιες) έχει ελάχιστη τιμή στο  (δηλαδή την μικρότερη επιτρεπτή τιμή του
(δηλαδή την μικρότερη επιτρεπτή τιμή του  ). Άρα η δοθείσα έχει μέγιστη τιμή
). Άρα η δοθείσα έχει μέγιστη τιμή 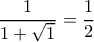 .
.  στην πλευρά
στην πλευρά  , δηλαδή ουσιαστικά ενώνουμε το
, δηλαδή ουσιαστικά ενώνουμε το  με το σημείο επαφής. Τότε τα ορθογώνια τρίγωνα
με το σημείο επαφής. Τότε τα ορθογώνια τρίγωνα  είναι όμοια και άρα
είναι όμοια και άρα  ή αλλιώς
ή αλλιώς 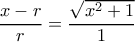 . Έπεται
. Έπεται 
 , οπότε το Ββ) άμεσο. Το σχήμα της είναι σαν το άνω μισό ενός
, οπότε το Ββ) άμεσο. Το σχήμα της είναι σαν το άνω μισό ενός  , με όριο
, με όριο  (άμεσο) καθώς
(άμεσο) καθώς 
 .
.  με το ίσον για
με το ίσον για  .
. .
. και
και  .
.