gbaloglou έγραψε: ↑Κυρ Μάιος 09, 2021 10:55 am
Με τις αποδείξεις του αρχικού προβλήματος ίσως ασχοληθώ αργότερα (αν έχω κάποια καλή ιδέα), όσον αφορά τα παραπάνω ισοπεριμετρικά: ενδιαφέροντα, αλλά όχι ακριβώς σχετιζόμενα προς το αρχικό πρόβλημα -- δεν ζητάμε δηλαδή το μέγιστο 'χορδικό εμβαδόν' που αντιστοιχεί σε όχι υποχρεωτικά κυκλικό τόξο δοθέντος μήκους, αλλά το μέγιστο 'χορδικό εμβαδόν' που αντιστοιχεί σε μεταβλητής γωνίας κυκλικό τόξο δοθέντος μήκους!
Νομίζω το να περιοριστούμε σε κυκλικά τόξα είναι υποσύνολο των καμπυλών του ισοπεριμετρικού προβλήματος, οπότε το ισοπεριμετρικό πρόβλημα είναι πιο γενικό αλλά όχι απαραίτητα διαφορετικό από αυτό που θέλουμε.
Έχουμε ως δεδομένο το σταθερό μήκος της λαμαρίνας

μέτρου. Έχουμε επίσης δεδομένο οτι θέλουμε να κατασκευάσουμε διατομή σχήματος κυκλικού τμήματος ( τόξου). Από όλα τα δυνατά σχήματα που μπορούμε να φτιάξουμε με την λαμαρίνα ήδη έχουμε περιοριστεί σε κυκλικά.
Αν προσδιορίσουμε πιο κομμάτι του κύκλου μας δίνει το μέγιστο εμβαδόν, τότε από αυτό μπορούμε να υπολογίσουμε και την ακτίνα που θέλουμε (το ζητούμενο, η κατασκευή). Αν για παραδειγμα προσδιορίσουμε ότι το μέγιστο εμβαδόν διατομής μας το δίνουν τα

του κύκλου, τότε η ακτίνα που ψάχνουμε θα είναι

.
Αν θεωρήσουμε ότι κάνουμε ημικυκλική διατομή, τότε για την ακτίνα

θα ισχύει

. Το εμβαδόν της διατομής

σε αυτή την περίπτωση είναι

.
Αν θέλουμε να φτιάξουμε όλο το κυκλικό τμήμα, δηλαδή να φτιάξουμε σωλήνα, τότε η ακτίνα

πρέπει να είναι

. Σε αυτήν την περίπτωση το αντίστοιχο εμβαδόν

είναι

.
Παρατηρούμε ότι έχουμε μικρότερο εμβαδόν διατομής από, ότι αν φτιάχναμε ημικύκλιο. Δηλαδή δεν μας συμφέρει να φτιάξουμε σωλήνα, αλλά ανοιχτό κανάλι.
Τώρα, έστω ότι το ημικύκλιο δεν είναι το καλύτερο δυνατό κανάλι, αλλά κάποιο άλλο τόξο

. Θεωρούμε το συμμετρικό του τόξο ως προς την ευθεία

και εξετάζουμε την καμπύλη

. Δηλαδή μια κλειστή καμπύλη (σωλήνα) μήκους

και εμβαδόν διατομής

.
Επίσης θεωρούμε και την αντίστοιχη κλειστή καμπύλη που προκύπτει από ημικύκλιο μήκους

. Αυτή θα έχει μήκος

και θα είναι ένας κύκλος. Με εμβαδόν

,

.
Όμως από όλες τις καμπύλες με μήκος

το μέγιστο εμβαδόν το έχει ο κύκλος απότε

, άτοπο.
Άρα δεν μπορεί να έχουμε κατι καλύτερο από ημικυκλική διατομή και η ζητούμενη ακτίνα είναι

Τα παραπάνω ήταν περισσότερο για τον τίτλο "προφανούς" και πως μπορούμε να δικαιολογήσουμε τον τίτλο.

- kopiastikh_apodeiksh_profanous.png (18.5 KiB) Προβλήθηκε 950 φορές
 .
. .
. ] 'Μικρή' διατομή = κυκλικός τομέας - τρίγωνο =
] 'Μικρή' διατομή = κυκλικός τομέας - τρίγωνο = 
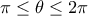 ] 'Μεγάλη' διατομή = κυκλικός τομέας + τρίγωνο =
] 'Μεγάλη' διατομή = κυκλικός τομέας + τρίγωνο = 
 για
για  .
. αρκεί βεβαίως να μελετηθεί ο αριθμητής
αρκεί βεβαίως να μελετηθεί ο αριθμητής 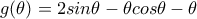 . Εδώ ... είτε κάποιο γραφιστικό πακέτο -- δεν συνιστώ την χρήση τους, όχι κατά την πρώτη ή δεύτερη προσπάθεια τουλάχιστον, σε όσους μαθαίνουν Λογισμό -- είτε η διακριτική υπόδειξη του θεματοδότη σε πιθανό συνδυασμό με την δική μας παρατηρητικότητα και εγρήγορση ... υποδεικνύουν πιθανό μέγιστο για
. Εδώ ... είτε κάποιο γραφιστικό πακέτο -- δεν συνιστώ την χρήση τους, όχι κατά την πρώτη ή δεύτερη προσπάθεια τουλάχιστον, σε όσους μαθαίνουν Λογισμό -- είτε η διακριτική υπόδειξη του θεματοδότη σε πιθανό συνδυασμό με την δική μας παρατηρητικότητα και εγρήγορση ... υποδεικνύουν πιθανό μέγιστο για  , και όντως
, και όντως  . Περαιτέρω διαίσθηση ή/και κοινή λογική συνιστούν
. Περαιτέρω διαίσθηση ή/και κοινή λογική συνιστούν  για
για  και
και  για
για  .
. και
και  : η πρώτη μας δίνει αύξουσα
: η πρώτη μας δίνει αύξουσα  για
για  (μέσω
(μέσω  και
και  ) και φθίνουσα
) και φθίνουσα  (μέσω
(μέσω  ,
,  ), η δεύτερη μας δίνει κυρτή
), η δεύτερη μας δίνει κυρτή  και κοίλη
και κοίλη  .
. προκύπτει η
προκύπτει η  και
και  .
. προκύπτει η
προκύπτει η  ,
,  .
. .
. ,
,  και
και  .
. η μέγιστη διατομή καναλιού είναι ημικυκλική, ακτίνας
η μέγιστη διατομή καναλιού είναι ημικυκλική, ακτίνας  και εμβαδού
και εμβαδού  .
. είναι ένα ισοσκελές τραπέζιο με
είναι ένα ισοσκελές τραπέζιο με  .
. ![\displaystyle{
\begin{tikzpicture}[scale=0.7]
\draw (0, 0) -- (5, 0) -- (8, 4) -- (-2.94, 4.04) -- cycle;
\draw[line width=1.7pt] (-3, 0) -- (8.5, 0);
\draw [shift={(5,0)},color=gray,fill=gray,fill opacity=0.1] (0,0) -- (0:0.6) arc (0:53.13:0.6) -- cycle;
\draw [shift={(0,0)},color=gray,fill=gray,fill opacity=0.1] (0,0) -- (126.04:0.6) arc (126.04:180:0.6) -- cycle;
\draw (0, 0) node[below]{A};
\draw (5, 0) node[below]{B};
\draw (8, 4) node[above]{\text{\gr Γ}};
\draw (-2.94, 4.04) node[above]{\text{\gr Δ}};
\draw (5.8, 0.3) node[]{\text{\gr θ}};
\draw (-0.7, 0.3) node[]{\text{\gr θ}};
\end{tikzpicture}
} \displaystyle{
\begin{tikzpicture}[scale=0.7]
\draw (0, 0) -- (5, 0) -- (8, 4) -- (-2.94, 4.04) -- cycle;
\draw[line width=1.7pt] (-3, 0) -- (8.5, 0);
\draw [shift={(5,0)},color=gray,fill=gray,fill opacity=0.1] (0,0) -- (0:0.6) arc (0:53.13:0.6) -- cycle;
\draw [shift={(0,0)},color=gray,fill=gray,fill opacity=0.1] (0,0) -- (126.04:0.6) arc (126.04:180:0.6) -- cycle;
\draw (0, 0) node[below]{A};
\draw (5, 0) node[below]{B};
\draw (8, 4) node[above]{\text{\gr Γ}};
\draw (-2.94, 4.04) node[above]{\text{\gr Δ}};
\draw (5.8, 0.3) node[]{\text{\gr θ}};
\draw (-0.7, 0.3) node[]{\text{\gr θ}};
\end{tikzpicture}
}](/forum/ext/geomar/texintegr/latexrender/pictures/9e884fc55a8e594d520096445142b532.png)
 είναι η γωνία που σχηματίζουν οι πλευρές
είναι η γωνία που σχηματίζουν οι πλευρές  και
και  με τη βάση του καναλιού τότε:
με τη βάση του καναλιού τότε:
 και έχει το μέγιστο εμβαδόν που μπορούμε να πετύχουμε με αυτή την σταθερή περίμετρο. Ως γνωστών όμως το μεγαλύτερο εμβαδόν με σταθερή περίμετρο το έχει ο κύκλος. Άτοπο.
και έχει το μέγιστο εμβαδόν που μπορούμε να πετύχουμε με αυτή την σταθερή περίμετρο. Ως γνωστών όμως το μεγαλύτερο εμβαδόν με σταθερή περίμετρο το έχει ο κύκλος. Άτοπο.  ^ μία διαφορά είναι ότι εκεί μπορούμε να 'κλείσουμε' το κανάλι προς τα πάνω, ενώ εδώ όχι. [Λάθος ... αν επιτραπεί η
^ μία διαφορά είναι ότι εκεί μπορούμε να 'κλείσουμε' το κανάλι προς τα πάνω, ενώ εδώ όχι. [Λάθος ... αν επιτραπεί η  ή/και
ή/και  !]
!] , και η επίλυση της
, και η επίλυση της  το επιβεβαιώνει αυτό.
το επιβεβαιώνει αυτό.  και αναζητείται η γωνία
και αναζητείται η γωνία  είναι η (κάτω) βάση του καναλιού -- όχι κατ' ανάγκην η μικρότερη βάση του ισοσκελούς τραπεζίου πλέον! -- και
είναι η (κάτω) βάση του καναλιού -- όχι κατ' ανάγκην η μικρότερη βάση του ισοσκελούς τραπεζίου πλέον! -- και  οι ίσες πλευρές, ισχύει η
οι ίσες πλευρές, ισχύει η  , ενώ η άλλη (επάνω) βάση ισούται προς
, ενώ η άλλη (επάνω) βάση ισούται προς  (όπου
(όπου  ) και το ύψος ισούται προς
) και το ύψος ισούται προς  . Συμπεραίνουμε ότι το εμβαδόν ισούται προς
. Συμπεραίνουμε ότι το εμβαδόν ισούται προς  , και μηδενίζοντας τις μερικές παραγώγους λαμβάνουμε
, και μηδενίζοντας τις μερικές παραγώγους λαμβάνουμε

 λαμβάνουμε
λαμβάνουμε  και
και  , αντίστοιχα, οπότε
, αντίστοιχα, οπότε  και εύκολα πλέον
και εύκολα πλέον  (οπότε άμεσα
(οπότε άμεσα  ) ... για μέγιστο εμβαδόν, που πρέπει να ελεγχθεί μέσω της 'γνωστής' ορίζουσας κλπ (παραλείπω τις λεπτομέρειες).
) ... για μέγιστο εμβαδόν, που πρέπει να ελεγχθεί μέσω της 'γνωστής' ορίζουσας κλπ (παραλείπω τις λεπτομέρειες). ) πλέον!
) πλέον! , σταθερό.
, σταθερό.
 έχει μέγιστο,
έχει μέγιστο, 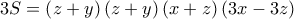 ,
,  , σταθερό, άρα παρουσιάζει μέγιστο όταν
, σταθερό, άρα παρουσιάζει μέγιστο όταν , δηλαδή όταν
, δηλαδή όταν  .
.
 έχει μέγιστο,
έχει μέγιστο,  ,
,  και
και  , δηλαδή όταν
, δηλαδή όταν ![\displaystyle {\rm E}\left( \theta \right) = \frac{{{T^2}}}{{2}} \cdot \frac{{\theta - \eta \mu \theta }}{{{\theta ^2}}},\;\;\theta \in \left( {0,\;2\pi } \right] \displaystyle {\rm E}\left( \theta \right) = \frac{{{T^2}}}{{2}} \cdot \frac{{\theta - \eta \mu \theta }}{{{\theta ^2}}},\;\;\theta \in \left( {0,\;2\pi } \right]](/forum/ext/geomar/texintegr/latexrender/pictures/a380b48823b411e1fcd43b4654ad5609.png)
![\displaystyle \theta \in \left( {0,\;2\pi } \right] \displaystyle \theta \in \left( {0,\;2\pi } \right]](/forum/ext/geomar/texintegr/latexrender/pictures/20767054866c2a3dffe655e9fa814e83.png) είναι
είναι 
![\displaystyle f:\left[ {0,\;2\pi } \right] \to R,\;\;f\left( x \right) = {x^2} - \pi x + \pi \eta \mu x \displaystyle f:\left[ {0,\;2\pi } \right] \to R,\;\;f\left( x \right) = {x^2} - \pi x + \pi \eta \mu x](/forum/ext/geomar/texintegr/latexrender/pictures/ed81ed58d64fe8c1aa424b0402a0ccfb.png)
 και
και 
 .
.  , οπότε εξίσωση έχει δύο ρίζες
, οπότε εξίσωση έχει δύο ρίζες  .
.![\displaystyle f''\left( x \right) > 0 \Leftrightarrow \eta \mu x < \frac{2}{\pi } \Leftrightarrow x \in \left[ {0,\;{\rho _1}} \right) \cup \left( {{\rho _2},2\pi } \right] \displaystyle f''\left( x \right) > 0 \Leftrightarrow \eta \mu x < \frac{2}{\pi } \Leftrightarrow x \in \left[ {0,\;{\rho _1}} \right) \cup \left( {{\rho _2},2\pi } \right]](/forum/ext/geomar/texintegr/latexrender/pictures/42e115037deb7389dd25af0aa7bbcd00.png)
 και
και  .
. φαίνονται στον πίνακα
φαίνονται στον πίνακα ![\displaystyle \forall x\left[ {0,\;2\pi } \right],\;\;f\left( x \right) \ge 0 \displaystyle \forall x\left[ {0,\;2\pi } \right],\;\;f\left( x \right) \ge 0](/forum/ext/geomar/texintegr/latexrender/pictures/c6fafa69bf89e6bafbe1359eacfc8544.png) , οπότε
, οπότε  , με το ίσον όταν
, με το ίσον όταν  .
. μέτρου. Έχουμε επίσης δεδομένο οτι θέλουμε να κατασκευάσουμε διατομή σχήματος κυκλικού τμήματος ( τόξου). Από όλα τα δυνατά σχήματα που μπορούμε να φτιάξουμε με την λαμαρίνα ήδη έχουμε περιοριστεί σε κυκλικά.
μέτρου. Έχουμε επίσης δεδομένο οτι θέλουμε να κατασκευάσουμε διατομή σχήματος κυκλικού τμήματος ( τόξου). Από όλα τα δυνατά σχήματα που μπορούμε να φτιάξουμε με την λαμαρίνα ήδη έχουμε περιοριστεί σε κυκλικά. του κύκλου, τότε η ακτίνα που ψάχνουμε θα είναι
του κύκλου, τότε η ακτίνα που ψάχνουμε θα είναι  .
. θα ισχύει
θα ισχύει  . Το εμβαδόν της διατομής
. Το εμβαδόν της διατομής  σε αυτή την περίπτωση είναι
σε αυτή την περίπτωση είναι  .
. . Σε αυτήν την περίπτωση το αντίστοιχο εμβαδόν
. Σε αυτήν την περίπτωση το αντίστοιχο εμβαδόν  .
. . Θεωρούμε το συμμετρικό του τόξο ως προς την ευθεία
. Θεωρούμε το συμμετρικό του τόξο ως προς την ευθεία  και εξετάζουμε την καμπύλη
και εξετάζουμε την καμπύλη  . Δηλαδή μια κλειστή καμπύλη (σωλήνα) μήκους
. Δηλαδή μια κλειστή καμπύλη (σωλήνα) μήκους  .
.  ,
,  .
. , άτοπο.
, άτοπο.
 , αν είναι ήδη διαθέσιμες οι
, αν είναι ήδη διαθέσιμες οι  και
και  , τότε αυτή που χρειαζόμαστε είναι άμεση από την
, τότε αυτή που χρειαζόμαστε είναι άμεση από την  . [Βεβαίως εδώ
. [Βεβαίως εδώ  = Ισοπεριμετρική ανισότητα,
= Ισοπεριμετρική ανισότητα,  = μέγιστη κυκλική διατομή,
= μέγιστη κυκλική διατομή,  , οπότε αρκεί να δειχθούν οι
, οπότε αρκεί να δειχθούν οι  και
και  για το τυχόν σημείο
για το τυχόν σημείο  όπου
όπου  και για το τυχόν σημείο
και για το τυχόν σημείο 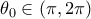 όπου
όπου  ,
,  .
. και
και 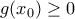 για το τυχόν σημείο
για το τυχόν σημείο  όπου
όπου  , τότε
, τότε  για
για  , με αντίστοιχο αποτέλεσμα για
, με αντίστοιχο αποτέλεσμα για 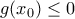 . Δεν εφαρμόζεται πάντοτε, διότι η ζητούμενη
. Δεν εφαρμόζεται πάντοτε, διότι η ζητούμενη  είναι συχνά υπερβολικά ισχυρή -- στην συγκεκριμένη περίπτωση ήμασταν ιδιαίτερα τυχεροί, καθώς όχι μόνον ισχύει αλλά είναι και τετριμμένη. (Να σημειωθεί επίσης ότι το σημείο τοπικού ακρότατου
είναι συχνά υπερβολικά ισχυρή -- στην συγκεκριμένη περίπτωση ήμασταν ιδιαίτερα τυχεροί, καθώς όχι μόνον ισχύει αλλά είναι και τετριμμένη. (Να σημειωθεί επίσης ότι το σημείο τοπικού ακρότατου  μπορεί να μην υπάρχει καν, στο συγκεκριμένο πρόβλημα για παράδειγμα υπάρχει στο
μπορεί να μην υπάρχει καν, στο συγκεκριμένο πρόβλημα για παράδειγμα υπάρχει στο  , ισχύει δηλαδή η
, ισχύει δηλαδή η 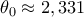 , αλλά όχι και στο
, αλλά όχι και στο  -- απόλυτα συμβατό αυτό με την μειωμένη δυσκολία επίλυσης στο δεύτερο διάστημα (αν ακολουθήσει κανείς είτε την αρχική μου απόδειξη είτε, πιθανολογώ εδώ, αυτήν του Γιώργου Ρίζου).]
-- απόλυτα συμβατό αυτό με την μειωμένη δυσκολία επίλυσης στο δεύτερο διάστημα (αν ακολουθήσει κανείς είτε την αρχική μου απόδειξη είτε, πιθανολογώ εδώ, αυτήν του Γιώργου Ρίζου).] -- τιμές της αρχικής συνάρτησης
-- τιμές της αρχικής συνάρτησης  στα σημεία όπου
στα σημεία όπου  , τιμές δηλαδή της
, τιμές δηλαδή της  -- τέμνει την αρχική συνάρτηση σε ένα ακριβώς σημείο στο
-- τέμνει την αρχική συνάρτηση σε ένα ακριβώς σημείο στο  )!
)!