 , σταθερού μήκους
, σταθερού μήκους  και το σημείο
και το σημείο  του
του  με
με  .
.Γράφουμε δύο ημικύκλια με ακτίνα
 και διάμετρο
και διάμετρο  , αντίστοιχα , τα οποία τέμνονται στο
, αντίστοιχα , τα οποία τέμνονται στο 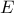 .
. Βρείτε το
 και τη γωνία
και τη γωνία  ώστε το
ώστε το  να είναι το μέγιστο δυνατό .
να είναι το μέγιστο δυνατό .Συντονιστής: KAKABASBASILEIOS
 , σταθερού μήκους
, σταθερού μήκους  και το σημείο
και το σημείο  του
του  με
με  .
. και διάμετρο
και διάμετρο  , αντίστοιχα , τα οποία τέμνονται στο
, αντίστοιχα , τα οποία τέμνονται στο 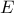 .
.  και τη γωνία
και τη γωνία  ώστε το
ώστε το  να είναι το μέγιστο δυνατό .
να είναι το μέγιστο δυνατό . έχουμε
έχουμε  και
και  άρα, αφού το
άρα, αφού το  είναι ορθογώνιο (βαίνει σε ημικύκλιο), έπεται ότι:
είναι ορθογώνιο (βαίνει σε ημικύκλιο), έπεται ότι:

 . Έχουμε:
. Έχουμε: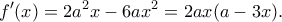
 για την οποία το ζητούμενο εμβαδό γίνεται μέγιστο είναι
για την οποία το ζητούμενο εμβαδό γίνεται μέγιστο είναι  , ενώ τότε έχουμε:
, ενώ τότε έχουμε:

Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 8 επισκέπτες