 κέντρου
κέντρου 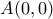 και ακτίνας
και ακτίνας  . Σημείο
. Σημείο  κινείται στο εσωτερικό της
κινείται στο εσωτερικό της  .
. Η κάθετη στην
 στο
στο  τέμνει το τόξο
τέμνει το τόξο  στο
στο  .
. α) Να βρεθεί η μέγιστη τιμή του
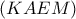 β) Να βρεθεί η μέγιστη τιμή του
β) Να βρεθεί η μέγιστη τιμή του 
Συντονιστής: KAKABASBASILEIOS
 κέντρου
κέντρου 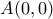 και ακτίνας
και ακτίνας  . Σημείο
. Σημείο  κινείται στο εσωτερικό της
κινείται στο εσωτερικό της  .
.  στο
στο  τέμνει το τόξο
τέμνει το τόξο  στο
στο  .
. 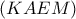 β) Να βρεθεί η μέγιστη τιμή του
β) Να βρεθεί η μέγιστη τιμή του 
Καλησπέρα Γιώργη! α)
 Η συνάρτηση
Η συνάρτηση  έχει παράγωγο
έχει παράγωγο  και παρουσιάζει για
και παρουσιάζει για  μέγιστο ίσο με
μέγιστο ίσο με 
 και με νόμο συνημιτόνου στο
και με νόμο συνημιτόνου στο 

 όπου
όπου 
 Και εδώ έχουμε μέγιστο για
Και εδώ έχουμε μέγιστο για
 ίσο με
ίσο με 
 είναι ισόπλευρο.
είναι ισόπλευρο. και το εμβαδόν του τραπεζίου θα είναι
και το εμβαδόν του τραπεζίου θα είναι 
 από το ορθογώνιο τρίγωνο
από το ορθογώνιο τρίγωνο  , λόγω συμπληρωματικότητας των γωνιών
, λόγω συμπληρωματικότητας των γωνιών 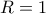 το εμβαδό ως συνάρτηση του
το εμβαδό ως συνάρτηση του  είναι
είναι 
 η οποία δίνει ώς λύσεις
η οποία δίνει ώς λύσεις 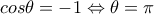 ή
ή 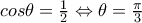

 και επειδή
και επειδή  και
και 
 και
και 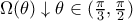
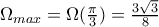
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες