 και την εφαπτομένη
και την εφαπτομένη  της γ.π. στο σημείο της
της γ.π. στο σημείο της  .
.Η
 τέμνει τους άξονες
τέμνει τους άξονες  στα
στα 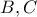 , αντίστοιχα.
, αντίστοιχα.α) Έστω
 το εμβαδόν του τριγώνου
το εμβαδόν του τριγώνου  . Να βρείτε το μέγιστο του
. Να βρείτε το μέγιστο του 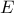
β) Να λύσετε την εξίσωση

Συντονιστής: KAKABASBASILEIOS
 και την εφαπτομένη
και την εφαπτομένη  της γ.π. στο σημείο της
της γ.π. στο σημείο της  .
. τέμνει τους άξονες
τέμνει τους άξονες  στα
στα 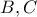 , αντίστοιχα.
, αντίστοιχα. το εμβαδόν του τριγώνου
το εμβαδόν του τριγώνου  . Να βρείτε το μέγιστο του
. Να βρείτε το μέγιστο του 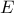

...γειά σου Γιώργη με τα ωραία σου..
 παραγωγίσιμη με
παραγωγίσιμη με  και η εφαπτομένη
και η εφαπτομένη  στο
στο  είναι
είναι  τέμνει τον
τέμνει τον  στο
στο  και τον
και τον  στο
στο  με
με  και
και  οπότε το εμβαδό του
οπότε το εμβαδό του  είναι
είναι
 που είναι παραγωγίσιμη με
που είναι παραγωγίσιμη με  και και
και και  και
και 
 άρα η
άρα η  γνήσια αύξουσα στο
γνήσια αύξουσα στο ![(0,\,\,\frac{1}{e}] (0,\,\,\frac{1}{e}]](/forum/ext/geomar/texintegr/latexrender/pictures/d237728a888e276a1780001ee2349a24.png) και
και  αφού
αφού  άρα η
άρα η  γνήσια φθίνουσα στο
γνήσια φθίνουσα στο  άρα στο
άρα στο  το εμβαδό παίρνει την μέγιστη τιμή με
το εμβαδό παίρνει την μέγιστη τιμή με 
 (1) και τώρα για την
(1) και τώρα για την ![h(x)=x\ln x-\frac{1}{e},\,\,x\in (0,\,1] h(x)=x\ln x-\frac{1}{e},\,\,x\in (0,\,1]](/forum/ext/geomar/texintegr/latexrender/pictures/15ba54924708463e378c9c71a43ba625.png) είναι παραγωγίσιμη με
είναι παραγωγίσιμη με ![h(x)=\ln x+1,\,\,x\in (0,\,1] h(x)=\ln x+1,\,\,x\in (0,\,1]](/forum/ext/geomar/texintegr/latexrender/pictures/c4ffb55263fe87b232ddf0cc9a93f8d5.png) και παρουσιάζει ελάχιστο στο
και παρουσιάζει ελάχιστο στο  (..εύκολα) άρα ισχύει
(..εύκολα) άρα ισχύει 
 οπότε (1) ισοδύναμα όταν
οπότε (1) ισοδύναμα όταν  και
και  αφού έχουμε άθροισμα μη αρνητικών αριθμών ίσο με το μηδέν επομένως λύση είναι το
αφού έχουμε άθροισμα μη αρνητικών αριθμών ίσο με το μηδέν επομένως λύση είναι το  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 20 επισκέπτες