![f:[a,b] \rightarrow \mathbb{R} f:[a,b] \rightarrow \mathbb{R}](/forum/ext/geomar/texintegr/latexrender/pictures/740e7fbdc78bd98d07847a9e74feae35.png) συνεχής συνάρτηση και παραγωγίσιμη στο
συνεχής συνάρτηση και παραγωγίσιμη στο  . Θεωρούμε ότι
. Θεωρούμε ότι  ,
,  . Δείξατε ότι για οποιουσδήποτε θετικούς αριθμούς
. Δείξατε ότι για οποιουσδήποτε θετικούς αριθμούς  υπάρχουν διακεκριμένοι αριθμοί
υπάρχουν διακεκριμένοι αριθμοί  τέτοιοι ώστε
τέτοιοι ώστε 
Συντονιστής: KAKABASBASILEIOS
![f:[a,b] \rightarrow \mathbb{R} f:[a,b] \rightarrow \mathbb{R}](/forum/ext/geomar/texintegr/latexrender/pictures/740e7fbdc78bd98d07847a9e74feae35.png) συνεχής συνάρτηση και παραγωγίσιμη στο
συνεχής συνάρτηση και παραγωγίσιμη στο  . Θεωρούμε ότι
. Θεωρούμε ότι  ,
,  . Δείξατε ότι για οποιουσδήποτε θετικούς αριθμούς
. Δείξατε ότι για οποιουσδήποτε θετικούς αριθμούς  υπάρχουν διακεκριμένοι αριθμοί
υπάρχουν διακεκριμένοι αριθμοί  τέτοιοι ώστε
τέτοιοι ώστε 

Τόλη πες την αλήθεια! Δεν ήθελες να την βάλεις σε αυτό τον φάκελο ε;Tolaso J Kos έγραψε: ↑Σάβ Αύγ 31, 2019 7:27 pmΈστωσυνεχής συνάρτηση και παραγωγίσιμη στο
. Θεωρούμε ότι
,
. Δείξατε ότι για οποιουσδήποτε θετικούς αριθμούς
υπάρχουν διακεκριμένοι αριθμοί
τέτοιοι ώστε

 μπορούμε να γράψουμε την προς απόδειξη σχέση ως
μπορούμε να γράψουμε την προς απόδειξη σχέση ως  όπου τώρα
όπου τώρα  και
και 
 στο
στο  ώστε
ώστε
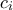 θα τα επιλέξουμε έτσι ώστε
θα τα επιλέξουμε έτσι ώστε 
 . Για να πετύχουμε τη δεύτερη θα πρέπει, επειδή
. Για να πετύχουμε τη δεύτερη θα πρέπει, επειδή  ,
, περιέχει το
περιέχει το  Από την υπόθεση αυτό δεν
Από την υπόθεση αυτό δεν ![g(x)=\dfrac{f(x(b-a)-a)-f(a)}{f(b)-f(a)}=\dfrac{f(x(b-a)+a)-f(a)}{b-a},x\in[0,1] g(x)=\dfrac{f(x(b-a)-a)-f(a)}{f(b)-f(a)}=\dfrac{f(x(b-a)+a)-f(a)}{b-a},x\in[0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/9161f648c6ed4970666678a4f0f6aa52.png) .
.  είναι συνεχής και επομένως
είναι συνεχής και επομένως ![(0,1)\subseteq g([0,1]).(\bigstar ) (0,1)\subseteq g([0,1]).(\bigstar )](/forum/ext/geomar/texintegr/latexrender/pictures/43f11e26c29430d106416f1cea5a65a0.png) To σημαντικότερο. Για την καινούρια συνάρτηση το συμπέρασμα παραμένει
To σημαντικότερο. Για την καινούρια συνάρτηση το συμπέρασμα παραμένει  για την
για την  υπάρχουν και
υπάρχουν και 
 και αντίστροφα. Άρα δουλεύουμε με την
και αντίστροφα. Άρα δουλεύουμε με την 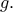 Παίρνουμε τώρα
Παίρνουμε τώρα  και επιλέγουμε
και επιλέγουμε 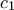 έτσι ώστε
έτσι ώστε  Το
Το 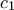 είναι εξασφαλισμένο από το γεγονός ότι
είναι εξασφαλισμένο από το γεγονός ότι  και από την
και από την 
 μπορούμε να επιλέξουμε
μπορούμε να επιλέξουμε  στο
στο  ώστε
ώστε  άρα και
άρα και  . Επαναλαμβάνουμε τη διαδικασία μέχρι το
. Επαναλαμβάνουμε τη διαδικασία μέχρι το 
 και ολοκληρώνουμε την απόδειξη με το ΘΜΤ.
και ολοκληρώνουμε την απόδειξη με το ΘΜΤ. μπορούμε να γράψουμε την προς απόδειξη σχέση ως
μπορούμε να γράψουμε την προς απόδειξη σχέση ως  όπου τώρα
όπου τώρα  και
και 
 δεν έχουμε να δείξουμε τίποτα γιατί μπορούμε να πάρουμε όποια σημεία θέλουμε.
δεν έχουμε να δείξουμε τίποτα γιατί μπορούμε να πάρουμε όποια σημεία θέλουμε.
 .
. μπορούμε να υποθέσουμε ότι
μπορούμε να υποθέσουμε ότι 
 μπορεί να επιλεγεί ώστε
μπορεί να επιλεγεί ώστε 
 διαφορετικά σημεία ώστε
διαφορετικά σημεία ώστε

 διαφορετικό των υπολοίπων ώστε
διαφορετικό των υπολοίπων ώστε 

 μπορεί να επιλεγεί ώστε
μπορεί να επιλεγεί ώστε 

Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες