 με τύπο
με τύπο  των πανελλαδικών εξετάσεων.
των πανελλαδικών εξετάσεων.Για ποιά
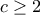 έχει λύση το σύστημα
έχει λύση το σύστημα ;
;Συντονιστής: KAKABASBASILEIOS
 με τύπο
με τύπο  των πανελλαδικών εξετάσεων.
των πανελλαδικών εξετάσεων.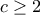 έχει λύση το σύστημα
έχει λύση το σύστημα ;
;ΕίναιAl.Koutsouridis έγραψε: ↑Σάβ Ιουν 29, 2019 3:09 pmΔίνεται η συνάρτησημε τύπο
των πανελλαδικών εξετάσεων.
Για ποιάέχει λύση το σύστημα
;
![f''(x)=\dfrac {2(x-1)[(x-1)^2+3]}{[(x-1)^2+1]^2} f''(x)=\dfrac {2(x-1)[(x-1)^2+3]}{[(x-1)^2+1]^2}](/forum/ext/geomar/texintegr/latexrender/pictures/408bc1b296697c55f0cacb53d42eb89d.png) ή
ή  .
. 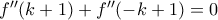 για κάθε πραγματικό
για κάθε πραγματικό  . Διαλέγουμε λοιπον
. Διαλέγουμε λοιπον 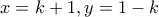 και τώρα για κάθε
και τώρα για κάθε  υπάρχει ζεύγος
υπάρχει ζεύγος  που ικανοποιεί την ζητούμενη.
που ικανοποιεί την ζητούμενη....καλησπέραAl.Koutsouridis έγραψε: ↑Σάβ Ιουν 29, 2019 3:09 pmΔίνεται η συνάρτησημε τύπο
των πανελλαδικών εξετάσεων.
Για ποιάέχει λύση το σύστημα
;
 και
και  και
και  και
και  επομένως η
επομένως η  παρουσιάζει μοναδικό σημείο καμπής το
παρουσιάζει μοναδικό σημείο καμπής το  .
. και
και  δηλαδή ισχύει
δηλαδή ισχύει 
 τότε για
τότε για  το ζεύγος
το ζεύγος  είναι λύση της εξίσωσης
είναι λύση της εξίσωσης  και για να είναι λύση και της
και για να είναι λύση και της  πρέπει
πρέπει 
 .
.  με δυο κατάλληλες μετατοπίσεις, μια προς τα αριστερά
με δυο κατάλληλες μετατοπίσεις, μια προς τα αριστερά (
( ) και μια προς τα κάτω κατά
) και μια προς τα κάτω κατά  μας δίνει την συνάρτηση
μας δίνει την συνάρτηση  , η οποία είναι εύκολο να παρατηρήσουμε ότι είναι περιττή. Άρα θα έχει κέντρο συμμετρίας το
, η οποία είναι εύκολο να παρατηρήσουμε ότι είναι περιττή. Άρα θα έχει κέντρο συμμετρίας το  και επομένως η
και επομένως η  θα έχει κέντρο συμμετρίας το σημείο
θα έχει κέντρο συμμετρίας το σημείο  .
.Σύμφωνα με την παραπάνω ιδιότητα θα έχουμεΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Πέμ Μάιος 09, 2019 1:49 pm
Τοείναι κέντρο συμμετρίας αν και μόνο αν
για κάθε πραγματικόείναι
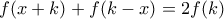


 είναι λύσεις της πρώτης εξίσωσης του συστήματος κτλ...
είναι λύσεις της πρώτης εξίσωσης του συστήματος κτλ...Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 7 επισκέπτες