 ;
;Άσκηση σχολικού
Συντονιστής: KAKABASBASILEIOS
Άσκηση σχολικού
Στην άσκηση 5,από τις γενικές ασκήσεις του διαφορικού λογισμού του σχολικού βιβλίου,πως εξηγείται θεωρητικά ότι το μεγαλύτερο δυνατό μήκος της σκάλας που μπορεί να μεταφερθεί οριζόντια ισοδυναμεί με την μικρότερη δυνατή τιμή του μήκους του  ;
;
 ;
;Λέξεις Κλειδιά:
-
Λάμπρος Κατσάπας
- Δημοσιεύσεις: 838
- Εγγραφή: Σάβ Ιουν 17, 2017 10:17 pm
- Τοποθεσία: Αθήνα
Re: Άσκηση σχολικού
Αν και προφανές...
Το μεγαλύτερο μήκος σκάλας που στρίβει είναι το μικρότερο μήκος σκάλας που δεν στρίβει.
Τα ''μεγαλύτερο'' και ''μικρότερο'' εντός εισαγωγικών.
Στο σχήμα της άσκησης έχει σκάλα που δεν στρίβει για μην χάνεται η επαφή και να μπορεί να δουλέψει γεωμετρικά.
Πιο αυστηρά: Είναι προφανές ότι δεν μπορεί να υπάρξουν σκάλες που ούτε στρίβουν ούτε δεν στρίβουν

Έστω
 το σύνολο των μηκών
το σύνολο των μηκών  των σκαλών που στρίβουν και
των σκαλών που στρίβουν και  το σύνολο των μηκών
το σύνολο των μηκών  των σκαλών που δεν στρίβουν. Αυτά είναι ξένα μεταξύ τους. Επίσης,
των σκαλών που δεν στρίβουν. Αυτά είναι ξένα μεταξύ τους. Επίσης, 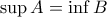 .
. Πράγματι, κάθε στοιχείο του
 είναι άνω φράγμα του
είναι άνω φράγμα του  δηλαδή για κάθε
δηλαδή για κάθε 
και για κάθε
 ισχύει
ισχύει  Άρα
Άρα  . Αν ήταν
. Αν ήταν 
τότε θα καταλήγαμε σε άτοπο από
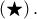
- Γιώργος Ρίζος
- Επιμελητής
- Δημοσιεύσεις: 5284
- Εγγραφή: Δευ Δεκ 29, 2008 1:18 pm
- Τοποθεσία: Κέρκυρα
Re: Άσκηση σχολικού
Καλησπέρα. Αντιγράφω από το σχόλιο που περιέχεται σε παρόμοιο πρόβλημα στην "Οδό Μαθηματικής Σκέψης".
Το ερώτημα της εκφώνησης ίσως να μη γίνεται άμεσα κατανοητό από όλους τους μαθητές. Μπορούμε να δώσουμε βοηθήσουμε τους μαθητές να κατανοήσουν το θέμα, περιγράφοντας την κίνηση της σκάλας ως εξής:
«Σέρνουμε τη σκάλα κατά μήκος του τοίχου στην ευθεία που ορίζουν τα Ο, Γ. Μόλις αγγίξει η σκάλα στο Γ, τη στρέφουμε με κέντρο περιστροφής το Ο, ώστε η μία της άκρη να αγγίζει τον τοίχο σε σημείο Α. Αν η άλλη άκρη αγγίξει το απέναντι τοίχο σε σημείο Β, τότε η σκάλα δεν μπορεί να στρίψει στη γωνία. Πρέπει, λοιπόν να έχει μήκος μικρότερο από το μικρότερο ευθύγραμμο τμήμα ΑΒ, που διέρχεται από το Ο».
edit: Να διευκρινίσω ότι δεν επιχειρώ θεωρητική εξήγηση, αντιθέτως δίνωμια παραστατική περιγραφή της κίνησης, παριστάνοντας τη σκάλα, ως ευθύγραμμο τμήμα, που δεν έχει πλάτος, ακολουθώντας το σχήμα του σχολικού βιβλίου. Στην Οδό Μαθηματικής Σκέψης, σε συνεχόμενο πρόβλημα μελετάται και η περίπτωση ορθογωνίου παραλληλογράμμου με το μέγιστο εμβαδό που θα μπορούσε να στρίψει στη γωνία.
Το ερώτημα της εκφώνησης ίσως να μη γίνεται άμεσα κατανοητό από όλους τους μαθητές. Μπορούμε να δώσουμε βοηθήσουμε τους μαθητές να κατανοήσουν το θέμα, περιγράφοντας την κίνηση της σκάλας ως εξής:
«Σέρνουμε τη σκάλα κατά μήκος του τοίχου στην ευθεία που ορίζουν τα Ο, Γ. Μόλις αγγίξει η σκάλα στο Γ, τη στρέφουμε με κέντρο περιστροφής το Ο, ώστε η μία της άκρη να αγγίζει τον τοίχο σε σημείο Α. Αν η άλλη άκρη αγγίξει το απέναντι τοίχο σε σημείο Β, τότε η σκάλα δεν μπορεί να στρίψει στη γωνία. Πρέπει, λοιπόν να έχει μήκος μικρότερο από το μικρότερο ευθύγραμμο τμήμα ΑΒ, που διέρχεται από το Ο».
edit: Να διευκρινίσω ότι δεν επιχειρώ θεωρητική εξήγηση, αντιθέτως δίνωμια παραστατική περιγραφή της κίνησης, παριστάνοντας τη σκάλα, ως ευθύγραμμο τμήμα, που δεν έχει πλάτος, ακολουθώντας το σχήμα του σχολικού βιβλίου. Στην Οδό Μαθηματικής Σκέψης, σε συνεχόμενο πρόβλημα μελετάται και η περίπτωση ορθογωνίου παραλληλογράμμου με το μέγιστο εμβαδό που θα μπορούσε να στρίψει στη γωνία.
τελευταία επεξεργασία από Γιώργος Ρίζος σε Τετ Μάιος 08, 2019 9:18 pm, έχει επεξεργασθεί 1 φορά συνολικά.
-
ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ
- Δημοσιεύσεις: 3600
- Εγγραφή: Πέμ Φεβ 27, 2014 9:05 am
- Τοποθεσία: ΧΑΛΚΙΔΑ- ΑΘΗΝΑ-ΚΡΗΤΗ
Re: Άσκηση σχολικού
Δεν εξηγείται θεωρητικά.
Εχουμε ένα πραγματικό πρόβλημα.
Η μόνη εξήγηση είναι να κάνουμε πείραμα.
Τα άλλα απλώς παραποιούν τα Μαθηματικά.
- Al.Koutsouridis
- Δημοσιεύσεις: 1797
- Εγγραφή: Πέμ Ιαν 30, 2014 11:58 pm
- Τοποθεσία: Αθήνα
Re: Άσκηση σχολικού
Δε ξέρω αν μπορούμε να το προσεγγίσουμε ως εξής το πρόβλημα:
Μπορούμε να θεωρήσουμε ότι η σκάλα αρχικά είναι παράλληλη στον οριζόντιο διάδρομο αρκετά μακριά από την γωνία. Αν δεν είναι τότε μπορούμε να την "οριζοντοποιήσουμε" (αν χωράει υπό κλίση ως προς το διάδρομο, τότε θα χωράει και οριζόντια). Ομοίως όταν περάσει στον κάθετο διάδρομο στην τελική θέση θα θεωρήσουμε ότι πάλι είναι παράλληλη στο διάδρομο. Θεωρούμε το μέσο της σκάλας, αυτό διαγράφει μια καμπύλη (θεωρούμε συνεχή) στους διαδρόμους . Σε κάθε σημείο αυτής της καμπύλης αντιστοιχούμε μια γωνία. Την γωνία που σχηματίζει η διεύθυνση της σκάλας με την διεύθυνση του οριζόντιου διαδρόμου. Η γωνία αυτή μεταβάλεται (θεωρούμε πάλι συνεχώς) από έως
έως  . Άρα κάποια στιγμή θα λάβει και την τιμή
. Άρα κάποια στιγμή θα λάβει και την τιμή  .
.
Για την τιμή εξετάζουμε ποιά είναι η μέγιστη σκάλα που μπορεί να έχουμε εσωτερικά των διαδρόμων. Αν η σκάλα δεν ακουμπά στους εξωτερικούς τοίχους των διαδρόμων, τότε μπορούμε να την προεκτείνουμε ώστε να ακουμπά. Άρα η μέγιστη σκάλα θα πρέπει να εφάπτεται των τοιχομάτων. Από όλες τις σκάλες που εφάπτονται των τοιχωμάτων, η σκάλα που εφάπτεται και της εσωτερικής γωνίας είναι η μεγαλύτερη. Αν η σκάλα είναι μακρύτερη τότε θα "τέμνει" τα τοιχώματα.
εξετάζουμε ποιά είναι η μέγιστη σκάλα που μπορεί να έχουμε εσωτερικά των διαδρόμων. Αν η σκάλα δεν ακουμπά στους εξωτερικούς τοίχους των διαδρόμων, τότε μπορούμε να την προεκτείνουμε ώστε να ακουμπά. Άρα η μέγιστη σκάλα θα πρέπει να εφάπτεται των τοιχομάτων. Από όλες τις σκάλες που εφάπτονται των τοιχωμάτων, η σκάλα που εφάπτεται και της εσωτερικής γωνίας είναι η μεγαλύτερη. Αν η σκάλα είναι μακρύτερη τότε θα "τέμνει" τα τοιχώματα.
Από την στιγμή που οπωσδήποτε θα υπάρχει γωνία , μεγαλύτερη σκάλα δεν μπορούμε να περάσουμε. Αρκεί λοιπόν να δείξουμε ότι σκάλα με μήκος
, μεγαλύτερη σκάλα δεν μπορούμε να περάσουμε. Αρκεί λοιπόν να δείξουμε ότι σκάλα με μήκος  μπορεί να περαστεί.
μπορεί να περαστεί.
Μπορούμε ισοδύναμα να το δούμε ως μια σκάλα που αρχικά είναι κατακόρυφα στηριγμένη στον ένα τοίχο και την αφήνουμε να γλιστρήσει στο οριζόντιο τοίχο (έδαφος). Το envelope της σκάλας μήκους σε αυτή την περίπτωση είναι μια αστεροειδής καμπύλη (σχέση 31) με εξίσωση
σε αυτή την περίπτωση είναι μια αστεροειδής καμπύλη (σχέση 31) με εξίσωση
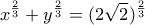
και να δείξουμε ότι βρίσκεται εσωτερικά των διαδρόμων .
.
Μπορούμε να θεωρήσουμε ότι η σκάλα αρχικά είναι παράλληλη στον οριζόντιο διάδρομο αρκετά μακριά από την γωνία. Αν δεν είναι τότε μπορούμε να την "οριζοντοποιήσουμε" (αν χωράει υπό κλίση ως προς το διάδρομο, τότε θα χωράει και οριζόντια). Ομοίως όταν περάσει στον κάθετο διάδρομο στην τελική θέση θα θεωρήσουμε ότι πάλι είναι παράλληλη στο διάδρομο. Θεωρούμε το μέσο της σκάλας, αυτό διαγράφει μια καμπύλη (θεωρούμε συνεχή) στους διαδρόμους . Σε κάθε σημείο αυτής της καμπύλης αντιστοιχούμε μια γωνία. Την γωνία που σχηματίζει η διεύθυνση της σκάλας με την διεύθυνση του οριζόντιου διαδρόμου. Η γωνία αυτή μεταβάλεται (θεωρούμε πάλι συνεχώς) από
 έως
έως  . Άρα κάποια στιγμή θα λάβει και την τιμή
. Άρα κάποια στιγμή θα λάβει και την τιμή  .
.Για την τιμή
 εξετάζουμε ποιά είναι η μέγιστη σκάλα που μπορεί να έχουμε εσωτερικά των διαδρόμων. Αν η σκάλα δεν ακουμπά στους εξωτερικούς τοίχους των διαδρόμων, τότε μπορούμε να την προεκτείνουμε ώστε να ακουμπά. Άρα η μέγιστη σκάλα θα πρέπει να εφάπτεται των τοιχομάτων. Από όλες τις σκάλες που εφάπτονται των τοιχωμάτων, η σκάλα που εφάπτεται και της εσωτερικής γωνίας είναι η μεγαλύτερη. Αν η σκάλα είναι μακρύτερη τότε θα "τέμνει" τα τοιχώματα.
εξετάζουμε ποιά είναι η μέγιστη σκάλα που μπορεί να έχουμε εσωτερικά των διαδρόμων. Αν η σκάλα δεν ακουμπά στους εξωτερικούς τοίχους των διαδρόμων, τότε μπορούμε να την προεκτείνουμε ώστε να ακουμπά. Άρα η μέγιστη σκάλα θα πρέπει να εφάπτεται των τοιχομάτων. Από όλες τις σκάλες που εφάπτονται των τοιχωμάτων, η σκάλα που εφάπτεται και της εσωτερικής γωνίας είναι η μεγαλύτερη. Αν η σκάλα είναι μακρύτερη τότε θα "τέμνει" τα τοιχώματα.Από την στιγμή που οπωσδήποτε θα υπάρχει γωνία
 , μεγαλύτερη σκάλα δεν μπορούμε να περάσουμε. Αρκεί λοιπόν να δείξουμε ότι σκάλα με μήκος
, μεγαλύτερη σκάλα δεν μπορούμε να περάσουμε. Αρκεί λοιπόν να δείξουμε ότι σκάλα με μήκος  μπορεί να περαστεί.
μπορεί να περαστεί. Μπορούμε ισοδύναμα να το δούμε ως μια σκάλα που αρχικά είναι κατακόρυφα στηριγμένη στον ένα τοίχο και την αφήνουμε να γλιστρήσει στο οριζόντιο τοίχο (έδαφος). Το envelope της σκάλας μήκους
 σε αυτή την περίπτωση είναι μια αστεροειδής καμπύλη (σχέση 31) με εξίσωση
σε αυτή την περίπτωση είναι μια αστεροειδής καμπύλη (σχέση 31) με εξίσωση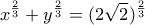
και να δείξουμε ότι βρίσκεται εσωτερικά των διαδρόμων
-
Λάμπρος Κατσάπας
- Δημοσιεύσεις: 838
- Εγγραφή: Σάβ Ιουν 17, 2017 10:17 pm
- Τοποθεσία: Αθήνα
Re: Άσκηση σχολικού
Δεν καταλαβαίνω το ''Τα άλλα απλώς παραποιούν τα Μαθηματικά''. Ποια είναι αυτά;ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Τετ Μάιος 08, 2019 8:35 pmΔεν εξηγείται θεωρητικά.
Εχουμε ένα πραγματικό πρόβλημα.
Η μόνη εξήγηση είναι να κάνουμε πείραμα.
Τα άλλα απλώς παραποιούν τα Μαθηματικά.
Επίσης, το πείραμα γιατί χρειάζεται να γίνει; Για να εξηγήσουμε το ''παράδοξο'' γιατί στη λύση του σχολικού
ελαχιστοποιεί συνάρτηση ενώ στην εκφώνηση ζητά μέγιστο μήκος;
Aν καταλαβαίνω καλά τον προβληματισμό της ann79, ας με διορθώσει αν κάνω λάθος, αυτός είναι.
Είναι προφανές ότι η λύση της άσκησης θεωρεί ότι υπάρχει μια οριακή κατάσταση όπου έχουμε σκάλα
που στρίβει και δεν στρίβει. Το πρόβλημα λύνεται εύκολα ελαχιστοποιήσουμε στο σύνολο των σκαλών που δεν
στρίβουν όπως στο σχήμα του βιβλίου (δεν το διευκρινίζει βέβαια αυτό το βιβλίο οπότε χρειάζεται κάποιος να
το συμπεράνει). Αν το πρόβλημα είναι πρακτικό μπορεί κάποιος να πάρει 100 σκάλες διαφόρων μηκών και να δοκιμάσει.
Έτσι μπορεί να προσεγγίσει το μέγιστο μήκος σκάλας. Η μαθηματική εξιδανίκευση του προβλήματος είναι πάντως αυτή.
-
ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ
- Δημοσιεύσεις: 3600
- Εγγραφή: Πέμ Φεβ 27, 2014 9:05 am
- Τοποθεσία: ΧΑΛΚΙΔΑ- ΑΘΗΝΑ-ΚΡΗΤΗ
Re: Άσκηση σχολικού
Υποτίθεται μιλάμε θεωρητικάΛάμπρος Κατσάπας έγραψε: ↑Τετ Μάιος 08, 2019 1:05 pmΑν και προφανές...
Το μεγαλύτερο μήκος σκάλας που στρίβει είναι το μικρότερο μήκος σκάλας που δεν στρίβει.
Τα ''μεγαλύτερο'' και ''μικρότερο'' εντός εισαγωγικών.
Στο σχήμα της άσκησης έχει σκάλα που δεν στρίβει για μην χάνεται η επαφή και να μπορεί να δουλέψει γεωμετρικά.
Πιο αυστηρά: Είναι προφανές ότι δεν μπορεί να υπάρξουν σκάλες που ούτε στρίβουν ούτε δεν στρίβουν
Έστωτο σύνολο των μηκών
των σκαλών που στρίβουν και
το σύνολο των μηκών
των σκαλών που δεν στρίβουν. Αυτά είναι ξένα μεταξύ τους. Επίσης,
.
Πράγματι, κάθε στοιχείο τουείναι άνω φράγμα του
δηλαδή για κάθε

και για κάθεισχύει
Άρα
. Αν ήταν

τότε θα καταλήγαμε σε άτοπο από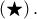
Γιατί αν δεν μιλάμε θεωρητικά τα πράγματα είναι απλά.
Αν κάποιοι δεν καταλαβαίνουν το πρόβλημα δεν πειράζει.(δεν αναφέρομαι
στον Λάμπρο αλλά στην ann79)
Δεν είναι ανάγκη όλοι να καταλαβαίνουν τα πάντα.
Θεωρητικά πως εξηγείται αυτό;Λάμπρος Κατσάπας έγραψε: ↑Τετ Μάιος 08, 2019 1:05 pmΠιο αυστηρά: Είναι προφανές ότι δεν μπορεί να υπάρξουν σκάλες που ούτε στρίβουν ούτε δεν στρίβουν
Γιατί δεν μπορεί μια σκάλα να μην στρίβει και μία με μεγαλύτερο μήκοςΛάμπρος Κατσάπας έγραψε: ↑Τετ Μάιος 08, 2019 1:05 pmΠράγματι, κάθε στοιχείο τουείναι άνω φράγμα του
δηλαδή για κάθε

και για κάθεισχύει

να στρίβει;
Φυσικά οι απαντήσεις στα παραπάνω είναι ότι αυτά λέει η κοινή λογική.
Μα αν εφαρμόσουμε την κοινή λογική τότε δεν χρειάζεται να γραφούν
τα παραπάνω που έγραψε ο Λάμπρος Κατσάπας.
Δηλαδή το πρόβλημα κατά την γνώμη μου είναι το ''θεωρητικά''
Το ''θεωρητικά'' στα Μαθηματικά είναι βαρεία κουβέντα.
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες
