 , για τις οποίες η εφαπτομένη στη γραφική παράσταση της συνάρτησης
, για τις οποίες η εφαπτομένη στη γραφική παράσταση της συνάρτησης ,
,που φέρεται από σημείο της με τετμημένη
 , να μην τέμνει καμία εκ των συναρτήσεων
, να μην τέμνει καμία εκ των συναρτήσεων  και
και  .
.Συντονιστής: KAKABASBASILEIOS
 , για τις οποίες η εφαπτομένη στη γραφική παράσταση της συνάρτησης
, για τις οποίες η εφαπτομένη στη γραφική παράσταση της συνάρτησης ,
, , να μην τέμνει καμία εκ των συναρτήσεων
, να μην τέμνει καμία εκ των συναρτήσεων  και
και  .
....Καλή χρονιάAl.Koutsouridis έγραψε: ↑Τετ Ιαν 02, 2019 1:02 pmΝα βρείτε όλες τις τιμές της παραμέτρου, για τις οποίες η εφαπτομένη στη γραφική παράσταση της συνάρτησης
,
που φέρεται από σημείο της με τετμημένη, να μην τέμνει καμία των συναρτήσεων
και
.
 πρώτα, για να έχουμε εφαπτομένη στη γραφική παράσταση της συνάρτησης,
πρώτα, για να έχουμε εφαπτομένη στη γραφική παράσταση της συνάρτησης,  , να μην τέμνει την συνάρτηση
, να μην τέμνει την συνάρτηση 


 είναι τότε:
είναι τότε:  ή
ή 

 που ισχύει για κάθε
που ισχύει για κάθε  .
. ότι
ότι  και
και 

 είναι
είναι  και
και 
 ισχύουν
ισχύουν 
 και κοίλη στο
και κοίλη στο  οπότε ισχύουν
οπότε ισχύουν 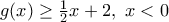 και
και  επομένως για να μην έχουν κοινά σημεία
επομένως για να μην έχουν κοινά σημεία  και η ευθεία
και η ευθεία  θα πρέπει να βρίσκεται στην ταινία που ορίζουν οι
θα πρέπει να βρίσκεται στην ταινία που ορίζουν οι  και
και  επομένως να ισχύει και
επομένως να ισχύει και  απ όπου
απ όπου  και
και  που ισχύει για κάθε
που ισχύει για κάθε  και αφού
και αφού  πρέπει
πρέπει 
 άρα
άρα
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 7 επισκέπτες