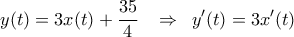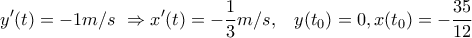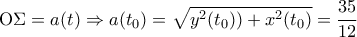Θεωρούμε τη συνάρτηση
 η οποία είναι παραγωγίσιμη στο
η οποία είναι παραγωγίσιμη στο  καθώς επίσης και τη συνάρτηση
καθώς επίσης και τη συνάρτηση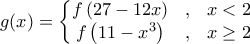
- Να δειχθεί ότι η
 είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο 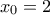 .
. - Αν είναι
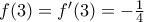 να βρεθεί η εξίσωση της εφαπτομένης της
να βρεθεί η εξίσωση της εφαπτομένης της  στο σημείο
στο σημείο 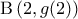 .
. - Σημείο
 με
με  κινείται επί της προηγούμενης ευθείας και πλησιάζει τον άξονα
κινείται επί της προηγούμενης ευθείας και πλησιάζει τον άξονα  με ρυθμό
με ρυθμό 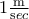 . Να βρεθεί ο ρυθμός μεταβολής της απόστασης
. Να βρεθεί ο ρυθμός μεταβολής της απόστασης  τη χρονική στιγμή κατά την οποία το
τη χρονική στιγμή κατά την οποία το  διέρχεται από το σημείο με τεταγμένη μηδέν.
διέρχεται από το σημείο με τεταγμένη μηδέν.


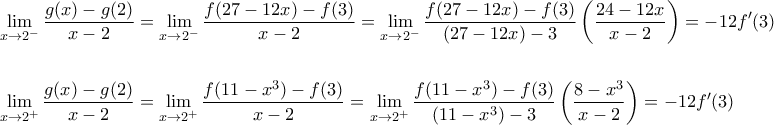
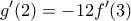
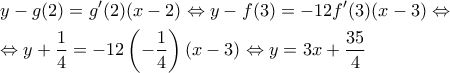
 . Τότε :
. Τότε :