Σελίδα 1 από 1
Μέγιστο εμβαδόν παραλληλογράμμου
Δημοσιεύτηκε: Δευ Ιούλ 09, 2018 1:10 am
από exdx
Δίνεται το τρίγωνο

και το σημείο

επί της

. Από το

φέρουμε

και από το
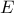
την

.
Ποια θέση του

επιτυγχάνει τη μεγιστοποίηση του
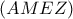
;
Δεκτή και η γεωμετρική αντιμετώπιση
Re: Μέγιστο εμβαδόν παραλληλογράμμου
Δημοσιεύτηκε: Δευ Ιούλ 09, 2018 2:12 am
από Μιχάλης Τσουρακάκης
exdx έγραψε: ↑Δευ Ιούλ 09, 2018 1:10 am
Δίνεται το τρίγωνο

και το σημείο

επί της

. Από το

φέρουμε

και από το
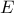
την

.
Ποια θέση του

επιτυγχάνει τη μεγιστοποίηση του
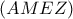
;
Δεκτή και η γεωμετρική αντιμετώπιση
άρση απόκρυψης

και

Αλλά

Άρα μέγιστο εμβαδόν έχουμε για το

που

δηλαδή για
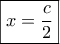

- mep.png (7.44 KiB) Προβλήθηκε 1061 φορές
Re: Μέγιστο εμβαδόν παραλληλογράμμου
Δημοσιεύτηκε: Δευ Ιούλ 09, 2018 8:51 am
από S.E.Louridas
Καλημέρα με καταρχάς μία γεωμετρική άποψη:
Το εμβαδόν του παραλληλογράμμου ισούται με
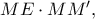
όπου
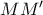
η απόσταση του

από την
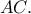
Όμως τα τρίγωνα

διατηρούν τις γωνίες τους, συνεπώς παραμένουν όμοια προς εαυτόν,
άρα έχουμε
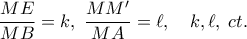
ή

Αρκεί λοιπόν το γινόμενο

να γίνει μέγιστο με

Αυτό ως γνωστόν επιτυγχάνεται όταν το

είναι μέσο της

Re: Μέγιστο εμβαδόν παραλληλογράμμου
Δημοσιεύτηκε: Δευ Ιούλ 09, 2018 1:50 pm
από Σταμ. Γλάρος
exdx έγραψε: ↑Δευ Ιούλ 09, 2018 1:10 am
Δίνεται το τρίγωνο

και το σημείο

επί της

. Από το

φέρουμε

και από το
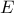
την

.
Ποια θέση του

επιτυγχάνει τη μεγιστοποίηση του
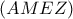
;
Δεκτή και η γεωμετρική αντιμετώπιση
Καλησπέρα . Μια προσπάθεια με Μαθηματικά Προσανατολισμού Γ΄Λυκείου ...

- Μέγιστο Εμβαδόν Παραλληλογράμμου.png (8.94 KiB) Προβλήθηκε 1061 φορές
To

κινείται επί της ευθείας

με
![x\in[0,2] x\in[0,2]](/forum/ext/geomar/texintegr/latexrender/pictures/84a1f4b719d95fedf2e65451bcbf7b30.png)
. Άρα

με
![t\in[0,2] t\in[0,2]](/forum/ext/geomar/texintegr/latexrender/pictures/190f82043c005f3fea7763655abe25d1.png)
.
Η ευθεία

είναι παράλληλη στον άξονα

και τέμνει την ευθεία

,στο

.
Όπου

η ευθεία, η οποία διέρχεται από τα

.
Εύκολα βρίσκουμε ότι
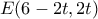
με
![t\in[0,2] t\in[0,2]](/forum/ext/geomar/texintegr/latexrender/pictures/190f82043c005f3fea7763655abe25d1.png)
.
Άρα
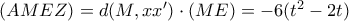
.
Θεωρώ την συνάρτηση
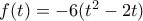
, παραγωγίσιμη με
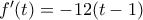
.
Με πίνακα μονοτονίας βρίσκουμε ότι η

παρουσιάζει μέγιστη τιμή στο

.
Συνεπώς η μεγιστοποίηση του
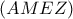
επιτυγχάνεται όταν

.
Δηλαδή, όπως απεδείχθη ήδη και γεωμετρικά

: μέσον της πλευράς

.
Φιλικά
Σταμ. Γλάρος
Re: Μέγιστο εμβαδόν παραλληλογράμμου
Δημοσιεύτηκε: Τρί Ιούλ 10, 2018 9:14 am
από S.E.Louridas
Μία προσπάθεια με ύλη Γ’ Λυκείου (Διαφορικoύ Λογισμού):
Θα εργαστούμε με βάση το σχήμα του Γιώργη.
Αν ονομάσουμε
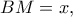
έχουμε:

και


από όπου προκύπτει ότι το μέγιστο επιτυγχάνεται όταν
 (*)
(*) Ευχόμενος βέβαια να μπορεί να χρησιμοποιηθεί η ομοιότητα τριγώνων και ο τύπος του εμβαδού τριγώνου, που δεν είναι στην ύλη της Γ' Λυκείου, χωρίς αυτό να είναι σε βάρος της κριτικής σκέψης ...
Re: Μέγιστο εμβαδόν παραλληλογράμμου
Δημοσιεύτηκε: Τρί Ιούλ 10, 2018 12:20 pm
από Γιώργος Ρίζος
Καλημέρα σε όλους. Μια ακόμα λύση με ομοιότητα και με μελέτη τριωνύμου. Νομίζω έτσι το αντιμετωπίζαμε, όταν είμαστε μαθητές πριν κάποιες δεκαετίες, τότε που οι παράγωγοι δεν είχαν την απόλυτη κυριαρχία στη σχολική ύλη.

- 10-07-2018 Γεωμετρία.jpg (18.86 KiB) Προβλήθηκε 938 φορές
Τα τρίγωνα
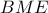
και

είναι όμοια, αφού έχουν δύο πλευρές συνευθειακές και τις τρίτες πλευρές τους παράλληλες.
Φέρνουμε το ύψος

που τέμνει κάθετα την

στο

.
Έστω

, οπότε και
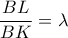
.
Τότε
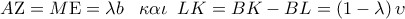
Είναι

.
Το μέγιστο του τμήματος της παραβολής
![\displaystyle y = - 2{x^2} + 2x,\;\;x \in \left[ {0,\;1} \right] \displaystyle y = - 2{x^2} + 2x,\;\;x \in \left[ {0,\;1} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/c1ca6551e6f29261d179c147faa5a8c4.png)
επιτυγχάνεται για

, οπότε για

έχουμε το μέγιστο εμβαδόν του παραλληλογράμμου

, δηλαδή όταν το

είναι μέσον του

.
edit: Να σημειώσω ότι ο
K.M. Tikhomirov στις «Ιστορίες για τα µέγιστα και ελάχιστα (σ.27 αγγλικής έκδοσης) αναφέρει ότι πρόκειται για το μοναδικό πρόβλημα μεγίστων-ελαχίστων στα
στοιχεία του Ευκλείδη, (σε μια σύγχρονη διατύπωσή του).
Re: Μέγιστο εμβαδόν παραλληλογράμμου
Δημοσιεύτηκε: Πέμ Ιούλ 12, 2018 1:20 am
από Γιώργος Μήτσιος
Καλημέρα σε όλους
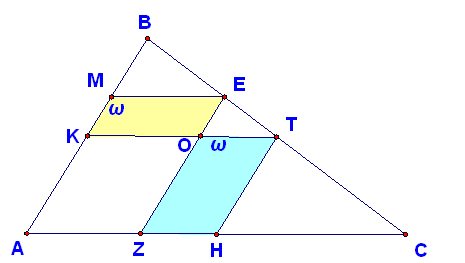
- Μέγιστο εμβαδόν.PNG (6.08 KiB) Προβλήθηκε 864 φορές
Τα

είναι τα μέσα των

.Έστω
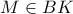
.
Θα δείξουμε ότι
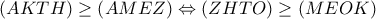
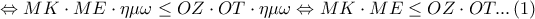
.
Aν

τότε

και λόγω της ομοιότητας των τριγώνων

είναι

.
Ακόμη

. Με χρήση αυτών η

που ισχύει.
Όμοια είναι η αντιμετώπιση αν

... Φιλικά Γιώργος
 και το σημείο
και το σημείο  επί της
επί της  . Από το
. Από το  φέρουμε
φέρουμε  και από το
και από το 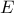 την
την  .
.  επιτυγχάνει τη μεγιστοποίηση του
επιτυγχάνει τη μεγιστοποίηση του 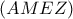 ;
; και το σημείο
και το σημείο  επί της
επί της  . Από το
. Από το  φέρουμε
φέρουμε  και από το
και από το 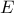 την
την  .
.  επιτυγχάνει τη μεγιστοποίηση του
επιτυγχάνει τη μεγιστοποίηση του 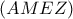 ;
; και
και 

 που
που  δηλαδή για
δηλαδή για 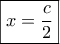
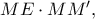 όπου
όπου 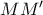 η απόσταση του
η απόσταση του  από την
από την 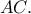
 διατηρούν τις γωνίες τους, συνεπώς παραμένουν όμοια προς εαυτόν,
διατηρούν τις γωνίες τους, συνεπώς παραμένουν όμοια προς εαυτόν, 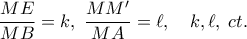 ή
ή 
 να γίνει μέγιστο με
να γίνει μέγιστο με 

 με
με ![x\in[0,2] x\in[0,2]](/forum/ext/geomar/texintegr/latexrender/pictures/84a1f4b719d95fedf2e65451bcbf7b30.png) . Άρα
. Άρα  με
με ![t\in[0,2] t\in[0,2]](/forum/ext/geomar/texintegr/latexrender/pictures/190f82043c005f3fea7763655abe25d1.png) .
. είναι παράλληλη στον άξονα
είναι παράλληλη στον άξονα  και τέμνει την ευθεία
και τέμνει την ευθεία  ,στο
,στο  .
. η ευθεία, η οποία διέρχεται από τα
η ευθεία, η οποία διέρχεται από τα  .
. 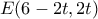 με
με 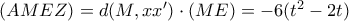 .
.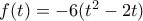 , παραγωγίσιμη με
, παραγωγίσιμη με 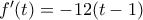 .
. παρουσιάζει μέγιστη τιμή στο
παρουσιάζει μέγιστη τιμή στο  .
. .
. .
.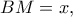 έχουμε:
έχουμε:  και
και 
 από όπου προκύπτει ότι το μέγιστο επιτυγχάνεται όταν
από όπου προκύπτει ότι το μέγιστο επιτυγχάνεται όταν 
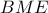 και
και  είναι όμοια, αφού έχουν δύο πλευρές συνευθειακές και τις τρίτες πλευρές τους παράλληλες.
είναι όμοια, αφού έχουν δύο πλευρές συνευθειακές και τις τρίτες πλευρές τους παράλληλες.  που τέμνει κάθετα την
που τέμνει κάθετα την  στο
στο  .
. , οπότε και
, οπότε και 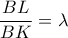 .
.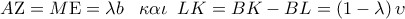
 .
.![\displaystyle y = - 2{x^2} + 2x,\;\;x \in \left[ {0,\;1} \right] \displaystyle y = - 2{x^2} + 2x,\;\;x \in \left[ {0,\;1} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/c1ca6551e6f29261d179c147faa5a8c4.png) επιτυγχάνεται για
επιτυγχάνεται για  , οπότε για
, οπότε για  έχουμε το μέγιστο εμβαδόν του παραλληλογράμμου
έχουμε το μέγιστο εμβαδόν του παραλληλογράμμου  , δηλαδή όταν το
, δηλαδή όταν το  είναι τα μέσα των
είναι τα μέσα των  .Έστω
.Έστω 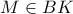 .
.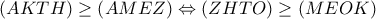
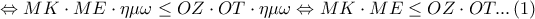 .
. τότε
τότε  και λόγω της ομοιότητας των τριγώνων
και λόγω της ομοιότητας των τριγώνων  είναι
είναι  .
.  . Με χρήση αυτών η
. Με χρήση αυτών η  που ισχύει.
που ισχύει.  ... Φιλικά Γιώργος
... Φιλικά Γιώργος