 και ένα σημείο
και ένα σημείο 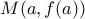 με
με  .
.Έστω
 η εφαπτόμενη της
η εφαπτόμενη της  στο
στο  η οποία τέμνει τους άξονες
η οποία τέμνει τους άξονες  στα
στα  , αντίστοιχα .
, αντίστοιχα .Φέρουμε
 ,
,  .
.α) Να προσδιορίσετε τη θέση του
 η οποία μεγιστοποιεί το εμβαδόν του τριγώνου
η οποία μεγιστοποιεί το εμβαδόν του τριγώνου  .
.β) Να αποδείξετε ότι στην ίδια θέση μεγιστοποείται και το εμβαδόν του ορθογωνίου
 .
.γ) Να βρείτε το οριακό μήκος του τμήματος
 , καθώς το
, καθώς το  .
.Edit : Διορθώθηκε το γ

 και
και 
 με
με 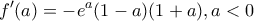
 παρουσιάζει για
παρουσιάζει για  μέγιστο
μέγιστο  Άρα η θέση του
Άρα η θέση του  είναι
είναι 
 με
με 
 μεγιστοποιείται
μεγιστοποιείται 
![\displaystyle ( - \infty , - 1] \displaystyle ( - \infty , - 1]](/forum/ext/geomar/texintegr/latexrender/pictures/fe78892af80df1769cff30671fb8e733.png) και γνησίως φθίνουσες στο
και γνησίως φθίνουσες στο ![\displaystyle [ - 1,0] \displaystyle [ - 1,0]](/forum/ext/geomar/texintegr/latexrender/pictures/c1e3e42d7bcaad024fc1b92e250e0e39.png)

 .
.


 .
.