 και
και  .
.α) Εξετάστε αν οι γραφικές τους παραστάσεις έχουν κοινές εφαπτόμενες .
β) Εξετάστε αν υπάρχουν σημεία των
 , με την ίδια τεταγμένη ,
, με την ίδια τεταγμένη ,στα οποία οι αγόμενες εφαπτόμενες να είναι παράλληλες .
Συντονιστής: KAKABASBASILEIOS
 και
και  .
. , με την ίδια τεταγμένη ,
, με την ίδια τεταγμένη , και
και  είναι παραγωγίσιμες στο πεδίο ορισμού τους με
είναι παραγωγίσιμες στο πεδίο ορισμού τους με  και έχουν εφαπτόμενες στα
και έχουν εφαπτόμενες στα  τις ευθείες
τις ευθείες και
και 
 ώστε
ώστε 




 είναι παραγωγίσιμη με
είναι παραγωγίσιμη με  και
και  και
και  γνήσια αύξουσα στο
γνήσια αύξουσα στο  και
και  γνήσια φθίνουσα στο
γνήσια φθίνουσα στο ![(1,\,\,{{e}^{e}}] (1,\,\,{{e}^{e}}]](/forum/ext/geomar/texintegr/latexrender/pictures/981ea0d9678bb74e245c79562f0cb120.png)
 την
την  που είναι και μοναδική ρίζα της
που είναι και μοναδική ρίζα της  άρα
άρα  και τότε στην
και τότε στην  όπου
όπου  έχουμε
έχουμε 

 , με την ίδια τεταγμένη ,
, με την ίδια τεταγμένη , με
με  που
που  και λόγω
και λόγω  να είναι
να είναι 
Μπορούμε τουλάχιστον το πρώτο να το δούμε γεωμετρικά.





Καλημέρα .
 η εφαπτομένη της
η εφαπτομένη της  , στο
, στο  .
. στο
στο  είναι
είναι  .
.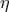 η εφαπτομένη της
η εφαπτομένη της  , στο
, στο  .
.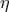 στο
στο  είναι
είναι  .
. και
και












 (1)
(1)  και
και  απορρίπτεται διότι
απορρίπτεται διότι  ,
,  συνεπώς
συνεπώς  .
. και
και  .
.



 (2)
(2) .
. , παραγωγίσιμη στο
, παραγωγίσιμη στο  με
με  .
. στο
στο  . Άρα η
. Άρα η  γνησίως φθίνουσα στο
γνησίως φθίνουσα στο ![(1, e^{e-1}] (1, e^{e-1}]](/forum/ext/geomar/texintegr/latexrender/pictures/7fa6f278956a6781204ca6fdd9d372b7.png) .
. . Άρα
. Άρα ![h\left (\left ( 1, e^{e-1} \right ] \right )= \left [ h\left (e^{e-1} \right ),+\infty \right ). h\left (\left ( 1, e^{e-1} \right ] \right )= \left [ h\left (e^{e-1} \right ),+\infty \right ).](/forum/ext/geomar/texintegr/latexrender/pictures/85aba13205fec055bb549ceea6a2d3e9.png)
 στο
στο  . Άρα η
. Άρα η  γνησίως αύξουσα στο
γνησίως αύξουσα στο  .
.![\displaystyle{\lim_{x\rightarrow+\infty }h(x)= \lim_{x\rightarrow +\infty }\left ( lnx\left [ (1-e)\dfrac{ln(lnx))}{lnx}+1-\dfrac{1}{lnx} \right ] \right )= +\infty} \displaystyle{\lim_{x\rightarrow+\infty }h(x)= \lim_{x\rightarrow +\infty }\left ( lnx\left [ (1-e)\dfrac{ln(lnx))}{lnx}+1-\dfrac{1}{lnx} \right ] \right )= +\infty}](/forum/ext/geomar/texintegr/latexrender/pictures/6fbe7b05d1ee02222fcade8fcbc204ad.png) ,
,  .
.
 .
. , παραγωγίσιμη στο
, παραγωγίσιμη στο  με
με  .
. παρουσιάζει στο
παρουσιάζει στο  , ολικό μέγιστο το
, ολικό μέγιστο το  .
. .
. έχει δύο ρίζες.
έχει δύο ρίζες. στο διάστημα
στο διάστημα ![(1, e^{e-1}] (1, e^{e-1}]](/forum/ext/geomar/texintegr/latexrender/pictures/7fa6f278956a6781204ca6fdd9d372b7.png) και η άλλη είναι η
και η άλλη είναι η  στο διάστημα
στο διάστημα  .
. και
και  , δηλαδή έχουμε τα σημεία
, δηλαδή έχουμε τα σημεία 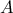 ,
,  όπως υπέδειξε ο KARKAR.
όπως υπέδειξε ο KARKAR. τότε και
τότε και  , δηλαδή έχουμε το κοινό σημείο των δύο συναρτήσεων που βρήκε ο Βασίλης. Εδώ οι εφαπτομένες ταυτίζονται.
, δηλαδή έχουμε το κοινό σημείο των δύο συναρτήσεων που βρήκε ο Βασίλης. Εδώ οι εφαπτομένες ταυτίζονται.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης