
Οριο
Συντονιστής: KAKABASBASILEIOS
-
ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ
- Δημοσιεύσεις: 3600
- Εγγραφή: Πέμ Φεβ 27, 2014 9:05 am
- Τοποθεσία: ΧΑΛΚΙΔΑ- ΑΘΗΝΑ-ΚΡΗΤΗ
-
Λάμπρος Κατσάπας
- Δημοσιεύσεις: 838
- Εγγραφή: Σάβ Ιουν 17, 2017 10:17 pm
- Τοποθεσία: Αθήνα
Re: Οριο
Θα χρησιμοποιήσω για ευκολία (δικιά μου) τους μετασχηματισμούς
 όπου
όπου 
Τότε η συνάρτηση γράφεται:


Όταν
 το
το 
Επίσης
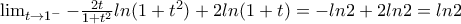 και με τον DLH δείχνουμε εύκολα ότι
και με τον DLH δείχνουμε εύκολα ότι 
Άρα το ζητούμενο όριο είναι ίσο με

Re: Οριο
Η αρχικη παράσταση έστω f(x)[\tex] γράφεται:





καθώς

συνεπώς το όριο της αρχικής με χρήση DLH για το κλάσμα καταλήγει:





καθώς





καθώς

συνεπώς το όριο της αρχικής με χρήση DLH για το κλάσμα καταλήγει:





καθώς

-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15762
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες

![\displaystyle \underset{x\to {{\frac{\pi }{2}}^{-}}}{\mathop{\lim }}\,\left[ \sin x\cdot \ln (\cos x)+\ln (\frac{1}{\cos x}+\tan x) \right] \displaystyle \underset{x\to {{\frac{\pi }{2}}^{-}}}{\mathop{\lim }}\,\left[ \sin x\cdot \ln (\cos x)+\ln (\frac{1}{\cos x}+\tan x) \right]](/forum/ext/geomar/texintegr/latexrender/pictures/a2b6a72771bc2c8de6e2b49168c503c4.png)

![\displaystyle \begin{array}{l}
\mathop {\lim }\limits_{u \to {0^ + }} \left[ {\cos u \cdot \ln (\sin u) + \ln (\frac{1}{{\sin u}} + \cot u)} \right] = \mathop {\lim }\limits_{u \to {0^ + }} \left[ {\cos u \cdot \ln (\sin u) + \ln \left( {\frac{{1 + \cos u}}{{\sin u}}} \right)} \right] = \\
\\
= \mathop {\lim }\limits_{u \to {0^ + }} [\cos u \cdot \ln (\sin u) + \ln (1 + \cos u) - \ln (\sin u)] = \\
\\
= \mathop {\lim }\limits_{u \to {0^ + }} \left( {\frac{{\cos u - 1}}{u}} \right) \cdot [u\ln (\sin u)] + \ln (1 + \cos u) = \ln 2
\end{array} \displaystyle \begin{array}{l}
\mathop {\lim }\limits_{u \to {0^ + }} \left[ {\cos u \cdot \ln (\sin u) + \ln (\frac{1}{{\sin u}} + \cot u)} \right] = \mathop {\lim }\limits_{u \to {0^ + }} \left[ {\cos u \cdot \ln (\sin u) + \ln \left( {\frac{{1 + \cos u}}{{\sin u}}} \right)} \right] = \\
\\
= \mathop {\lim }\limits_{u \to {0^ + }} [\cos u \cdot \ln (\sin u) + \ln (1 + \cos u) - \ln (\sin u)] = \\
\\
= \mathop {\lim }\limits_{u \to {0^ + }} \left( {\frac{{\cos u - 1}}{u}} \right) \cdot [u\ln (\sin u)] + \ln (1 + \cos u) = \ln 2
\end{array}](/forum/ext/geomar/texintegr/latexrender/pictures/ba6b128a58c0d0a58eca8ab26926d905.png)
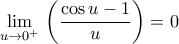 και
και  (αφού
(αφού 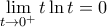 )
)![\displaystyle \underset{u\to {{0}^{+}}}{\mathop{\lim }}\,[\ln (1+\cos u)]=\ln 2 \displaystyle \underset{u\to {{0}^{+}}}{\mathop{\lim }}\,[\ln (1+\cos u)]=\ln 2](/forum/ext/geomar/texintegr/latexrender/pictures/ab7e8025b4758966f2d39fa14cfd7f77.png)
 , οπότε
, οπότε  και, ως γνωστόν,
και, ως γνωστόν,  έχουμε ότι η δοθείσα ισούται
έχουμε ότι η δοθείσα ισούται
