Σελίδα 1 από 1
Εύρεση τύπου
Δημοσιεύτηκε: Τρί Ιαν 23, 2018 9:11 am
από drakpap
Θα ήθελα μια βοήθεια στην εξής άσκηση αν μια συνάρτηση f δύο φορες παρμ/η στο R και ισχύουν
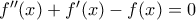
για κάθε

καθώς και
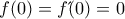
Να βρεθεί ο τύπος της f.
Ευχαριστώ εκ των προτέρων
Re: Εύρεση τύπου
Δημοσιεύτηκε: Τρί Ιαν 23, 2018 9:45 am
από Tolaso J Kos
drakpap έγραψε: ↑Τρί Ιαν 23, 2018 9:11 am
Θα ήθελα μια βοήθεια στην εξής άσκηση αν μια συνάρτηση f δύο φορες παρμ/η στο R και ισχύουν
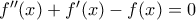
για κάθε

καθώς και
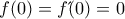
Να βρεθεί ο τύπος της f.
Ευχαριστώ εκ των προτέρων
Για να την προσπαθήσεις σου δίδω υπόδειξη:
Δείξε ότι η

δε μπορεί να έχει θετικό μέγιστο στο τυχόν

αλλά και ούτε αρνητικό ελάχιστο. Συμπέρανε ότι η

είναι η μηδενική συνάρτηση.
Προσθήκη αρκετή ώρα αργότερα:
Υποθέτουμε ότι η

παρουσιάζει θετικό μέγιστο, στο

. Τότε
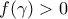
και
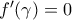
. Από το κριτήριο της δεύτερης παραγώγου είναι

. Η αρχική σχέση τότε θα δώσει:

το οποίο είναι άτοπο. Όμοια και αν υποθέσεις ότι έχει αρνητικό ελάχιστο. Το συμπέρασμα έπεται.
Re: Εύρεση τύπου
Δημοσιεύτηκε: Τρί Ιαν 23, 2018 8:48 pm
από ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ
Tolaso J Kos έγραψε: ↑Τρί Ιαν 23, 2018 9:45 am
drakpap έγραψε: ↑Τρί Ιαν 23, 2018 9:11 am
Θα ήθελα μια βοήθεια στην εξής άσκηση αν μια συνάρτηση f δύο φορες παρμ/η στο R και ισχύουν
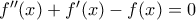
για κάθε

καθώς και
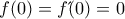
Να βρεθεί ο τύπος της f.
Ευχαριστώ εκ των προτέρων
Για να την προσπαθήσεις σου δίδω υπόδειξη:
Δείξε ότι η

δε μπορεί να έχει θετικό μέγιστο στο τυχόν

αλλά και ούτε αρνητικό ελάχιστο. Συμπέρανε ότι η

είναι η μηδενική συνάρτηση.
Προσθήκη αρκετή ώρα αργότερα:
Υποθέτουμε ότι η

παρουσιάζει θετικό μέγιστο, στο

. Τότε
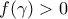
και
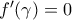
. Από το κριτήριο της δεύτερης παραγώγου είναι

. Η αρχική σχέση τότε θα δώσει:

το οποίο είναι άτοπο. Όμοια και αν υποθέσεις ότι έχει αρνητικό ελάχιστο. Το συμπέρασμα έπεται.
Αν η

είναι γνησίως αύξουσα στο

και γνησίως αύξουσα στο
![(-\infty ,0] (-\infty ,0]](/forum/ext/geomar/texintegr/latexrender/pictures/f9d75a40b8eadac31117745d2255ef61.png)
τότε τι αξία έχει το παραπάνω;
Εννοείται ότι είναι τοπικά μέγιστα-ελάχιστα και δεν είναι το

.
Να σημειώσω βέβαια ότι στην λύση που γνωρίζω χρειάζονται οι παρατηρήσεις σου Τόλη.
Αλλά δεν προκύπτει τετριμμένα από αυτές.
Re: Εύρεση τύπου
Δημοσιεύτηκε: Παρ Ιαν 26, 2018 11:16 pm
από ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ
Επαναφέρω την άσκηση.
Θεωρώ αρκετά δύσκολο αν όχι αδύνατο να λυθεί χωρίς χρήση ολοκληρωτικού λογισμού.
Στην ουσία ζητείται να αποδειχθεί το θεώρημα μονοσημάντου για Διαφορικές Εξισώσεις
σε μια ειδική περίπτωση.
Δεν γράφω προς το παρόν λύση με την ελπίδα να την χαρεί κάποιος άλλος.
Re: Εύρεση τύπου
Δημοσιεύτηκε: Σάβ Ιαν 27, 2018 12:27 am
από matha
Θέτουμε
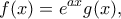
όπου το

θα το διαλέξουμε αργότερα. Φυσικά είναι
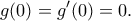
Τότε είναι
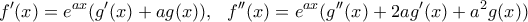
, οπότε η συνθήκη γράφεται
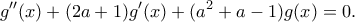
Αν λοιπόν διαλέξουμε ως

μια ρίζα της εξίσωσης
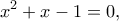
η συνθήκη γίνεται

(λόγω των

),
άρα η συνάρτηση
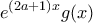
είναι σταθερή, οπότε μηδενική. Επομένως είναι
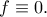
Re: Εύρεση τύπου
Δημοσιεύτηκε: Δευ Ιαν 29, 2018 11:15 pm
από ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ
matha έγραψε: ↑Σάβ Ιαν 27, 2018 12:27 am
Θέτουμε
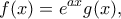
όπου το

θα το διαλέξουμε αργότερα. Φυσικά είναι
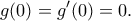
Τότε είναι
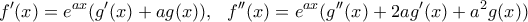
, οπότε η συνθήκη γράφεται
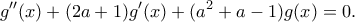
Αν λοιπόν διαλέξουμε ως

μια ρίζα της εξίσωσης
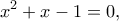
η συνθήκη γίνεται

(λόγω των

),
άρα η συνάρτηση
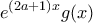
είναι σταθερή, οπότε μηδενική. Επομένως είναι
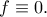

και λίγο είναι.
Re: Εύρεση τύπου
Δημοσιεύτηκε: Δευ Ιαν 29, 2018 11:45 pm
από Mihalis_Lambrou
drakpap έγραψε: ↑Τρί Ιαν 23, 2018 9:11 am
Θα ήθελα μια βοήθεια στην εξής άσκηση αν μια συνάρτηση f δύο φορες παρμ/η στο R και ισχύουν
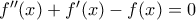
για κάθε

καθώς και
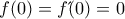
Να βρεθεί ο τύπος της f.
.
Αλλιώς: Αν

ρίζα της
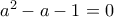
, η εξίσωση γράφεται
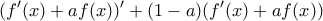
(που είναι της μορφής

).
Άρα
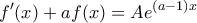
, που από τις
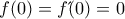
δίνει

. Άρα

, οπότε
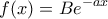
, που από την

δίνει

. Τελικά,

.
Re: Εύρεση τύπου
Δημοσιεύτηκε: Τετ Φεβ 07, 2018 1:02 am
από Παπαστεργίου Κώστας
Νομίζω ότι μια λύση με το μετασχηματισμό του D' Alembert όπως αυτή του κ Μάγγου και η παραλλαγή του κ Λάμπρου φαντάζει ασύλληπτη στο νου ενός μαθητή. Επιτρέψτε μου να δώσω μια δική μου που πιστεύω ότι είναι πιο κατανοητή και σίγουρα γενικότερη.
Να λυθεί η εξίσωση
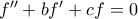
(1) όταν
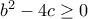
Αν
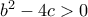
τότε η εξίσωση
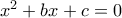
έχει δυο ρίζες

και
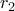
με
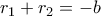
και
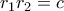
οπότε η (1) γίνεται

οπότε

και

Στην περίπτωση

τα πράγματα είναι πιο εύκολα διότι έχουμε μια ρίζα

και η (1) γίνεται
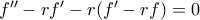
και εύκολα παίρνουμε
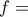

ΠΚ
Re: Εύρεση τύπου
Δημοσιεύτηκε: Τετ Φεβ 07, 2018 8:44 am
από Mihalis_Lambrou
Παπαστεργίου Κώστας έγραψε: ↑Τετ Φεβ 07, 2018 1:02 am
η παραλλαγή του κ Λάμπρου φαντάζει
ασύλληπτη στο νου ενός μαθητή. Επιτρέψτε μου να δώσω
μια δική μου που πιστεύω ότι είναι πιο κατανοητή και σίγουρα γενικότερη.
Χάνω κάτι;
Αυτό που έκανα είναι ακριβώς το ίδιο με αυτό που γράφεις. Μάλιστα κατά τι ευκολότερο γιατί τα
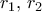
είναι ειδικοί αριθμοί, όπως δίνονται, και όχι η προφανής γενίκευση. Ας προσθέσω ότι οι τεχνικές αυτές είναι στάνταρ, χιλιοειπωμένες, που υπάρχουν στην μία ή την άλλη μορφή σε όλα τα βιβλία Διαφορικών Εξισώσεων.
Re: Εύρεση τύπου
Δημοσιεύτηκε: Πέμ Φεβ 08, 2018 12:38 pm
από Παπαστεργίου Κώστας
Mihalis_Lambrou έγραψε: ↑Τετ Φεβ 07, 2018 8:44 am
Παπαστεργίου Κώστας έγραψε: ↑Τετ Φεβ 07, 2018 1:02 am
η παραλλαγή του κ Λάμπρου φαντάζει
ασύλληπτη στο νου ενός μαθητή. Επιτρέψτε μου να δώσω
μια δική μου που πιστεύω ότι είναι πιο κατανοητή και σίγουρα γενικότερη.
Χάνω κάτι;
Αυτό που έκανα είναι ακριβώς το ίδιο με αυτό που γράφεις. Μάλιστα κατά τι ευκολότερο γιατί τα
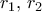
είναι ειδικοί αριθμοί, όπως δίνονται, και όχι η προφανής γενίκευση. Ας προσθέσω ότι οι τεχνικές αυτές είναι στάνταρ, χιλιοειπωμένες, που υπάρχουν στην μία ή την άλλη μορφή σε όλα τα βιβλία Διαφορικών Εξισώσεων.
Αμ δεν είναι το ίδιο. Αναφέρεσαι μόνο στην
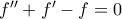
όπου παρουσιάζεις, ως από μηχανής θεό, τη ρίζα της

, δεν εξηγείς γιατί αυτή και όχι την

ούτε πως έφτασες στην
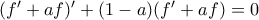
. Σε μαθητές απευθύνεσαι.
Με ρωτάς αν χάνεις κάτι. Την ψυχραιμία σου σίγουρα. Για κάτι άλλο ψάξτο μόνος σου. Σου χαρίζω τον τελευταίο λόγο.
Re: Εύρεση τύπου
Δημοσιεύτηκε: Πέμ Φεβ 08, 2018 3:14 pm
από Mihalis_Lambrou
Παπαστεργίου Κώστας έγραψε: ↑Πέμ Φεβ 08, 2018 12:38 pm
Με ρωτάς αν χάνεις κάτι. Την ψυχραιμία σου σίγουρα. Για κάτι άλλο ψάξτο μόνος σου. Σου χαρίζω τον τελευταίο λόγο.
Καλύτερα να μένουμε μόνο στα επιστημονικά θέματα και στο επίπεδο που έχει καθιερωθεί στο φόρουμ.
Στο θέμα μας.
Θέλεις να πει ότι το
είναι λιγότερο ουρανοκατέβατο από το
Το αφήνω στην κρίση των αναγνωστών.
Για μένα τα δύο είναι ουσιαστικά το ίδιο πράγμα. Μη τι άλλο το δεύτερο είναι ειδική περίπτωση του πρώτου, και άρα κάπως ευκολότερο.
Το όλο θέμα είναι έτσι και αλλιώς απλούστατο, οπότε δεν βλέπω πώς στοιχειοθετείται το σχόλιο περί ουρανοκατέβατου. Καλό είναι όταν κάνουμε Μαθηματικά, να μην μένουμε στα τυποποιημένα γιατί τότε μας φαίνονται όλα ουρανοκατέβατα.
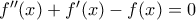

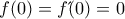
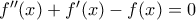

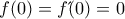
 δε μπορεί να έχει θετικό μέγιστο στο τυχόν
δε μπορεί να έχει θετικό μέγιστο στο τυχόν  αλλά και ούτε αρνητικό ελάχιστο. Συμπέρανε ότι η
αλλά και ούτε αρνητικό ελάχιστο. Συμπέρανε ότι η  . Τότε
. Τότε 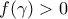 και
και 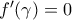 . Από το κριτήριο της δεύτερης παραγώγου είναι
. Από το κριτήριο της δεύτερης παραγώγου είναι  . Η αρχική σχέση τότε θα δώσει:
. Η αρχική σχέση τότε θα δώσει:
 και γνησίως αύξουσα στο
και γνησίως αύξουσα στο ![(-\infty ,0] (-\infty ,0]](/forum/ext/geomar/texintegr/latexrender/pictures/f9d75a40b8eadac31117745d2255ef61.png)
 .
.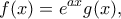 όπου το
όπου το  θα το διαλέξουμε αργότερα. Φυσικά είναι
θα το διαλέξουμε αργότερα. Φυσικά είναι 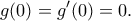
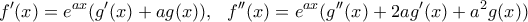 , οπότε η συνθήκη γράφεται
, οπότε η συνθήκη γράφεται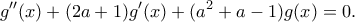
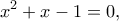 η συνθήκη γίνεται
η συνθήκη γίνεται (λόγω των
(λόγω των  ),
), 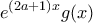 είναι σταθερή, οπότε μηδενική. Επομένως είναι
είναι σταθερή, οπότε μηδενική. Επομένως είναι 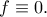
 ρίζα της
ρίζα της 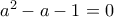 , η εξίσωση γράφεται
, η εξίσωση γράφεται 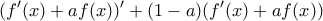 (που είναι της μορφής
(που είναι της μορφής  ).
). 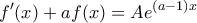 , που από τις
, που από τις  . Άρα
. Άρα  , οπότε
, οπότε 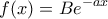 , που από την
, που από την  δίνει
δίνει  . Τελικά,
. Τελικά,  .
.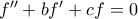 (1) όταν
(1) όταν 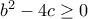
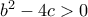 τότε η εξίσωση
τότε η εξίσωση 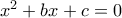 έχει δυο ρίζες
έχει δυο ρίζες  και
και 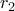 με
με 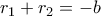 και
και 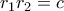 οπότε η (1) γίνεται
οπότε η (1) γίνεται οπότε
οπότε και
και 
 τα πράγματα είναι πιο εύκολα διότι έχουμε μια ρίζα
τα πράγματα είναι πιο εύκολα διότι έχουμε μια ρίζα  και η (1) γίνεται
και η (1) γίνεται 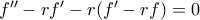
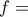

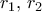 είναι ειδικοί αριθμοί, όπως δίνονται, και όχι η προφανής γενίκευση. Ας προσθέσω ότι οι τεχνικές αυτές είναι στάνταρ, χιλιοειπωμένες, που υπάρχουν στην μία ή την άλλη μορφή σε όλα τα βιβλία Διαφορικών Εξισώσεων.
είναι ειδικοί αριθμοί, όπως δίνονται, και όχι η προφανής γενίκευση. Ας προσθέσω ότι οι τεχνικές αυτές είναι στάνταρ, χιλιοειπωμένες, που υπάρχουν στην μία ή την άλλη μορφή σε όλα τα βιβλία Διαφορικών Εξισώσεων.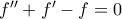 όπου παρουσιάζεις, ως από μηχανής θεό, τη ρίζα της
όπου παρουσιάζεις, ως από μηχανής θεό, τη ρίζα της  , δεν εξηγείς γιατί αυτή και όχι την
, δεν εξηγείς γιατί αυτή και όχι την  ούτε πως έφτασες στην
ούτε πως έφτασες στην 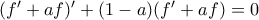 . Σε μαθητές απευθύνεσαι.
. Σε μαθητές απευθύνεσαι.