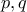 είναι συνεχείς στο
είναι συνεχείς στο  και
και  είναι λύσεις της εξίσωσης
είναι λύσεις της εξίσωσης  , όπου
, όπου 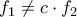 όπου
όπου  σταθερά, να αποδείξετε ότι ανάμεσα σε δύο διαδοχικές ρίζες της
σταθερά, να αποδείξετε ότι ανάμεσα σε δύο διαδοχικές ρίζες της  υπάρχει μοναδική ρίζα της
υπάρχει μοναδική ρίζα της  .
.Συντονιστής: KAKABASBASILEIOS
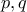 είναι συνεχείς στο
είναι συνεχείς στο  και
και  είναι λύσεις της εξίσωσης
είναι λύσεις της εξίσωσης  , όπου
, όπου 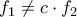 όπου
όπου  σταθερά, να αποδείξετε ότι ανάμεσα σε δύο διαδοχικές ρίζες της
σταθερά, να αποδείξετε ότι ανάμεσα σε δύο διαδοχικές ρίζες της  υπάρχει μοναδική ρίζα της
υπάρχει μοναδική ρίζα της  .
.Για λόγους ευκολίας σε κάποια σημεία θα παραλείπω ταΠρωτοπαπάς Λευτέρης έγραψε: ↑Δευ Νοέμ 06, 2017 5:24 pmΑν οι συναρτήσειςείναι συνεχείς στο
και
είναι λύσεις της εξίσωσης
, όπου
όπου
σταθερά, να αποδείξετε ότι ανάμεσα σε δύο διαδοχικές ρίζες της
υπάρχει μοναδική ρίζα της
.



 την δεύτερη με
την δεύτερη με 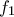




 τότε προκύπτει ότι
τότε προκύπτει ότι 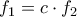
 οπότε
οπότε  (1)στο
(1)στο 
 δύο διαδοχικές ρίζες της
δύο διαδοχικές ρίζες της 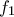
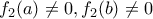
 δεν έχει ρίζα στο
δεν έχει ρίζα στο  τότε ορίζεται η
τότε ορίζεται η ![h=\dfrac{f_{1}}{f_{2}}:[a,b]\rightarrow \mathbb{R} h=\dfrac{f_{1}}{f_{2}}:[a,b]\rightarrow \mathbb{R}](/forum/ext/geomar/texintegr/latexrender/pictures/f2b36dc5ce9c8cfdbe6b8ae1b042dfb4.png)



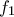 υπάρχει ρίζα της
υπάρχει ρίζα της  .
.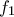

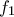 στο
στο  ΑΤΟΠΟ.
ΑΤΟΠΟ.ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Δευ Νοέμ 06, 2017 6:24 pmΓια λόγους ευκολίας σε κάποια σημεία θα παραλείπω ταΠρωτοπαπάς Λευτέρης έγραψε: ↑Δευ Νοέμ 06, 2017 5:24 pmΑν οι συναρτήσειςείναι συνεχείς στο
και
είναι λύσεις της εξίσωσης
, όπου
όπου
σταθερά, να αποδείξετε ότι ανάμεσα σε δύο διαδοχικές ρίζες της
υπάρχει μοναδική ρίζα της
.
Είναι
και
πολλαπλασιάζοντας την πρώτη μετην δεύτερη με
και αφαιρώντας προκύπτει
Θέτοντας
η προηγούμενη γίνεται
Αρα
Αντότε προκύπτει ότι
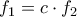
Αραοπότε
(1)στο
Εστωδύο διαδοχικές ρίζες της
Λόγω της (1) είναι
Αν ηδεν έχει ρίζα στο
τότε ορίζεται η
Είναι
οπότε από Rolle υπάρχει
με
ΑΤΟΠΟ λόγω της (1)
Αρα μεταξύ δύο διαδοχικών ριζών τηςυπάρχει ρίζα της
.
Αυτή είναι μοναδική γιατί αν υπήρχαν δύο τότε αλλάζοντας τους ρόλους των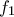
θα είχαμε ρίζα τηςστο
ΑΤΟΠΟ.
Σχόλιο.
Είναι γνωστό Θεώρημα των Διαφορικών Εξισώσεων(έχει και όνομα αλλά εγώ δεν το θυμάμαι)
Πολύ θα ήθελα να δω μια λύση που να χρησιμοποιεί μόνοΠρωτοπαπάς Λευτέρης έγραψε: ↑Τρί Νοέμ 07, 2017 11:33 pmΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Δευ Νοέμ 06, 2017 6:24 pmΓια λόγους ευκολίας σε κάποια σημεία θα παραλείπω ταΠρωτοπαπάς Λευτέρης έγραψε: ↑Δευ Νοέμ 06, 2017 5:24 pmΑν οι συναρτήσειςείναι συνεχείς στο
και
είναι λύσεις της εξίσωσης
, όπου
όπου
σταθερά, να αποδείξετε ότι ανάμεσα σε δύο διαδοχικές ρίζες της
υπάρχει μοναδική ρίζα της
.
Είναι
και
πολλαπλασιάζοντας την πρώτη μετην δεύτερη με
και αφαιρώντας προκύπτει
Θέτοντας
η προηγούμενη γίνεται
Αρα
Αντότε προκύπτει ότι
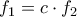
Αραοπότε
(1)στο
Εστωδύο διαδοχικές ρίζες της
Λόγω της (1) είναι
Αν ηδεν έχει ρίζα στο
τότε ορίζεται η
Είναι
οπότε από Rolle υπάρχει
με
ΑΤΟΠΟ λόγω της (1)
Αρα μεταξύ δύο διαδοχικών ριζών τηςυπάρχει ρίζα της
.
Αυτή είναι μοναδική γιατί αν υπήρχαν δύο τότε αλλάζοντας τους ρόλους των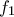
θα είχαμε ρίζα τηςστο
ΑΤΟΠΟ.
Σχόλιο.
Είναι γνωστό Θεώρημα των Διαφορικών Εξισώσεων(έχει και όνομα αλλά εγώ δεν το θυμάμαι)
1) Υπάρχει παρόμοιο θεώρημα και λέγεται θεώρημα Sturm. Έχει προφανώς άλλη εκφώνηση που αφορά φοιτητές.
2) Το αόριστο ολοκλήρωμα είναι εδώ και κάτι χρόνια εκτός ύλης.
3) Στην προτελευταία γραμμή, είτε υπάρχει τυπογραφικό λάθος (μάλλον λείπει ένα κόμμα) είτε λάθος στη λύση.
4) Η λύση προφανώς και είναι ημιτελής αφού μας διαβάζουν μαθητές.
 αντί γιά
αντί γιά  , όπου
, όπου  για κάθε
για κάθε  , όλα τώρα γίνονται νόμιμα.
, όλα τώρα γίνονται νόμιμα.Γεια σου Χρήστο.Christos.N έγραψε: ↑Τρί Ιούλ 30, 2019 1:07 pmΔηλαδή αν στηριχθούμε εδώ:
DeepinScreenshot_select-area_20190730130042.png
και μιλάω για την υποσημείωση στο τέλος, τότε ο Σταύρος αν είχε θεωρήσειαντί γιά
, όπου
για κάθε
, όλα τώρα γίνονται νόμιμα.
 τότε προκύπτει ότι
τότε προκύπτει ότι 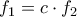
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 12 επισκέπτες