 για
για  είναι παραγωγίσιμη και στο
είναι παραγωγίσιμη και στο  με παράγωγο
με παράγωγο  ;
;Συντονιστής: KAKABASBASILEIOS
Το πεδίο ορισμού είναι τοann79 έγραψε:Καλημέρα. Πως αποδεικνύεται ότι η συνάρτησηγια
είναι παραγωγίσιμη και στο
με παράγωγο
;
 εφόσον
εφόσον  με
με  .
.
Μάριε, καλή η πρόθεσή σου να απαντήσεις. Έχεις όμως σκεφθεί ότι όταν απαντάς σε απολύτως τετριμμένα θέματα όπου ο ερωτών δεν αφιέρωσε ούτε γραμμάριο ουσιαστικής σκέψης, τότε κάνεις περισσότερη ζημιά από καλό;MarKo έγραψε:Το πεδίο ορισμού είναι τοann79 έγραψε:Καλημέρα. Πως αποδεικνύεται ότι η συνάρτησηγια
είναι παραγωγίσιμη και στο
με παράγωγο
;
εφόσον
με
.
Με τον ορισμό της παραγώγου εφόσον το 0 ανήκει στο πεδίο ορισμού , έχουμε:
Νομίζω πως είναι ευκαιρία να ξεκαθαρίσουμε κάποια πράγματα σχετικά με τη συνάρτησηann79 έγραψε:Καλημέρα. Πως αποδεικνύεται ότι η συνάρτησηγια
είναι παραγωγίσιμη και στο
με παράγωγο
;
 .
. εννοούμε
εννοούμε  η οποία είναι ορισμένη μόνο για
η οποία είναι ορισμένη μόνο για 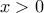 . Είναι το ευρύτερο δυνατό σύνολο όπου η
. Είναι το ευρύτερο δυνατό σύνολο όπου η  έχει έννοια ανεξαρτήτως
έχει έννοια ανεξαρτήτως  .
. μόνο για
μόνο για 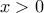
 αυτό το Π.Ο. μπορεί να επεκταθεί όπως πχ για
αυτό το Π.Ο. μπορεί να επεκταθεί όπως πχ για  όπου η
όπου η 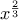 έχει έννοια σ όλο το
έχει έννοια σ όλο το  .
. με
με και
και  και αυτής να ζητήσουμε την παράγωγο στο μηδέν δια του ορισμού όπως πιο πάνω. Μάλιστα είναι
και αυτής να ζητήσουμε την παράγωγο στο μηδέν δια του ορισμού όπως πιο πάνω. Μάλιστα είναι  οπότε επεκτείνεται και ο προηγούμενος τύπος παραγωγίσεως.
οπότε επεκτείνεται και ο προηγούμενος τύπος παραγωγίσεως.  . Ίσως άλλη φορά.
. Ίσως άλλη φορά.Μέλη σε αυτήν τη Δ. Συζήτηση: Google [Bot] και 6 επισκέπτες