Σελίδα 1 από 1
και μια εξίσωση..
Δημοσιεύτηκε: Τρί Απρ 21, 2009 9:10 am
από giannisn1990
Να λυθεί στο
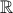
η παρακάτω εξίσωση

Re: και μια εξίσωση..
Δημοσιεύτηκε: Τρί Απρ 21, 2009 10:20 am
από hsiodos
Την έχω δει και σε άλλη ιστοσελίδα . Δίνω στο επισυναπτόμενο την ίδια υπόδειξη που έκανα εκεί με επιφύλαξη για τυχόν λάθος.
Γιώργος
Re: και μια εξίσωση..
Δημοσιεύτηκε: Τρί Απρ 21, 2009 10:20 am
από chris_gatos
Kαλημέρα σε όλους...
Μια προσέγγιση στην εξίσωση του Γιάννη...
Απο τη γνωστή τριγωνομετρική ταυτότητα sin2a=2sinacosa λαμβάνουμε :

αλλά και :

.
Αρα η εξίσωση γίνεται:

και καταλήγει στη μορφή :

(1).
Έστω

.
Tότε και η f αλλά και η g είναι γνησίως φθίνουσες...( 0<sinπ/12<1 και 0<cosπ/12<1 )
Συνεπώς :

.
Δηλαδή :

.
Με όμοιο τρόπο αν

, προκύπτει :

.
Αρα η μοναδική περίπτωση να ισχύει η (1) είναι αν και μόνο αν

.
Υ.Γ Για να είμαι ειλικρινής εγώ δεν την έχω δεί πουθενά αλλού.
Re: και μια εξίσωση..
Δημοσιεύτηκε: Τρί Απρ 21, 2009 10:42 am
από hsiodos
Ωραία η αντιμετώπιση της εξίσωσης στην τελική της μορφή Χρήστο.
Μας απαλλάσσει από τον κόπο να θεωρήσουμε συνάρτηση και να βρούμε την μονοτονία της(αυτό με παίδεψε λίγο).
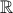 η παρακάτω εξίσωση
η παρακάτω εξίσωση 
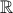 η παρακάτω εξίσωση
η παρακάτω εξίσωση 
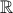 η παρακάτω εξίσωση
η παρακάτω εξίσωση 

 .
.
 (1).
(1). .
. .
. .
. , προκύπτει :
, προκύπτει : .
. .
.