 : Να δειχθεί , χωρίς χρήση λογαριθμικών
: Να δειχθεί , χωρίς χρήση λογαριθμικών πινάκων , ότι η εξίσωση :
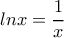 , έχει μοναδική ρίζα στο
, έχει μοναδική ρίζα στο  , ( αντί του
, ( αντί του  ) .
) .Συντονιστής: KAKABASBASILEIOS
 : Να δειχθεί , χωρίς χρήση λογαριθμικών
: Να δειχθεί , χωρίς χρήση λογαριθμικών 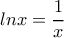 , έχει μοναδική ρίζα στο
, έχει μοναδική ρίζα στο  , ( αντί του
, ( αντί του  ) .
) .Με περίσσευμα και το
 . Πράγματι για
. Πράγματι για  ισχύει
ισχύει 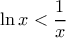 (καθώς ισοδυναμεί με το αληθές
(καθώς ισοδυναμεί με το αληθές  ) ενώ για
) ενώ για  έχουμε την ανάποδη ανισότητα (ισοδυμναμεί με την
έχουμε την ανάποδη ανισότητα (ισοδυμναμεί με την  ή αλλιώς
ή αλλιώς  , που σημαίνει
, που σημαίνει 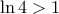 ή αλλιώς
ή αλλιώς  ).
).Θα μπορούσαμε, στον συγκεκριμένο φάκελο, να περιορίσουμε τη λύση στο διάστημα
 χωρίς τη χρήση λογισμικού; (Δεν το έχω εξετάσει).
χωρίς τη χρήση λογισμικού; (Δεν το έχω εξετάσει).Ακόμα καλύτερα όρια από ταgeorge visvikis έγραψε: ↑Πέμ Ιουν 17, 2021 11:08 amΘα μπορούσαμε, στον συγκεκριμένο φάκελο, να περιορίσουμε τη λύση στο διάστημαχωρίς τη χρήση λογισμικού; (Δεν το έχω εξετάσει).
 είναι τα
είναι τα  . Τα έχω ελέγξει χωρίς λογισμικό. Οι πράξεις είναι κάπως μεγάλες για διαγώνισμα σε τάξη αλλά δεν είναι ιδιαίτερα επίπονες.
. Τα έχω ελέγξει χωρίς λογισμικό. Οι πράξεις είναι κάπως μεγάλες για διαγώνισμα σε τάξη αλλά δεν είναι ιδιαίτερα επίπονες. και το
και το  .
.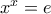 , και η ρίζα της είναι ο αριθμός :
, και η ρίζα της είναι ο αριθμός : 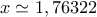
 .
. , καθώς και ότι :
, καθώς και ότι : 
 - διάστημα :
- διάστημα :  , είναι εύκολο να το δει κανείς ,
, είναι εύκολο να το δει κανείς , , ενώ :
, ενώ :  .
.Καλημέρα σας
 στο
στο  .
. .
. , το
, το  .
. στο
στο  τέμνει τον
τέμνει τον  στο
στο  .
. , την εν λόγω εφαπτομένη και τον άξονα
, την εν λόγω εφαπτομένη και τον άξονα  , είναι
, είναι
 .
.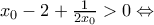
 .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες