ΘΕΜΑ Β
(Β1) Πρέπει

και

.
Επομένως,

και

. Άρα, οι
 δεν
δεν είναι ίσες. Για κάθε

έχουμε ότι:

Άρα, στο εν λόγω διάστημα οι δύο συναρτήσεις είναι ίσες και μάλιστα το συγκεκριμένο διάστημα είναι και το ευρύτερο δυνατό υποσύνολο του

, που αυτές είναι ίσες.
(Β2) Έχουμε ότι:

Άρα

.
Επιπλέον:

και άρα

.
Επίσης,

.
Άρα, οι δύο συναρτήσεις έχουν ίδια πεδία ορισμού και ίδιο τύπο άρα είναι ίσες.
(Β3) i. Έστω

,

. Η απόσταση του

από την αρχή των αξόνων δίνεται από τη σχέση:

ii. Για κάθε

έχουμε ότι

, άρα

άρτια.
Για κάθε

με

. Τότε

και

. Άρα,

. Άρα,

γνησίως φθίνουσα στο
![\left ( -\infty ,0 \right ] \left ( -\infty ,0 \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/1a80e9bfb475072dc3d68009b3d51d21.png)
.
Όμοια, για

με

είναι

. Άρα,

γνησίως αύξουσα στο

.
iii. Για

από το προηγούμενο ερώτημα η

είναι άυξουσα άρα και

.
![\displaystyle h\left ( x \right )=2\sqrt[8]{3}=h\left ( \sqrt[8]{3} \right )\Leftrightarrow x=\sqrt[8]{3} \displaystyle h\left ( x \right )=2\sqrt[8]{3}=h\left ( \sqrt[8]{3} \right )\Leftrightarrow x=\sqrt[8]{3}](/forum/ext/geomar/texintegr/latexrender/pictures/96edd3d066245f1dac9a570ef888f5ad.png)
.
Για

από το προηγούμενο ερώτημα η

είναι φθίνουσα άρα και

.
![\displaystyle h\left ( x \right )=2\sqrt[8]{3}=h\left (- \sqrt[8]{3} \right )\Leftrightarrow x=-\sqrt[8]{3} \displaystyle h\left ( x \right )=2\sqrt[8]{3}=h\left (- \sqrt[8]{3} \right )\Leftrightarrow x=-\sqrt[8]{3}](/forum/ext/geomar/texintegr/latexrender/pictures/a68713b045730e7a839692c886c94c89.png)
Επομένως, το ζητούμενο σημείο είναι το
![\displaystyle M\left ( \sqrt[8]{3},\sqrt[8]{3^{5}} \right ) \displaystyle M\left ( \sqrt[8]{3},\sqrt[8]{3^{5}} \right )](/forum/ext/geomar/texintegr/latexrender/pictures/2ac46dfa4db39bf522f144d57815cb33.png)
ή το
![\displaystyle M\left ( -\sqrt[8]{3},-\sqrt[8]{3^{5}} \right ) \displaystyle M\left ( -\sqrt[8]{3},-\sqrt[8]{3^{5}} \right )](/forum/ext/geomar/texintegr/latexrender/pictures/6256b17b80fb26982c63cf35d52900dd.png)
.
Φιλικά,
Μάριος
Υ.Γ. Μένει η λύση στο ΘΕΜΑ Δ. Θα αφήσω μερικές μέρες ακόμα μήπως κάποιος μαθητής ή συνάδελφος θέλει να μοιραστεί τη λύση του.
 στο θέμα Γ.
στο θέμα Γ.
 οπότε
οπότε
 παίρνουμε
παίρνουμε  το οποίο αντίκειται στο ότι η συνάρτηση
το οποίο αντίκειται στο ότι η συνάρτηση  είναι μη σταθερή. Τελικά
είναι μη σταθερή. Τελικά  .
.
 με
με  . Τότε:
. Τότε:
 . Έστω
. Έστω 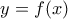 . Τότε:
. Τότε:
 άρα
άρα  . Συνεπώς
. Συνεπώς  και
και 
 υπάρχει
υπάρχει  τέτοιο ώστε
τέτοιο ώστε  ενώ
ενώ  υπάρχει
υπάρχει  τέτοιο ώστε
τέτοιο ώστε  . Άρα για
. Άρα για  είναι
είναι  και εφόσον η
και εφόσον η  η οποία είναι γνησίως αύξουσα. Το αποτέλεσμα έπεται από Bolzano σε συνδυασμό με το ερώτημα (γ).
η οποία είναι γνησίως αύξουσα. Το αποτέλεσμα έπεται από Bolzano σε συνδυασμό με το ερώτημα (γ).
 πραγματικό είναι
πραγματικό είναι  . Αφού η
. Αφού η  θα υπάρχουν
θα υπάρχουν  ώστε
ώστε  και
και  . Άρα για την συνεχή συνάρτηση
. Άρα για την συνεχή συνάρτηση  ισχύει
ισχύει  και άρα από Bolzano έχουμε την ύπραξη της ρίζας. Τώρα η μοναδικότητα έρχεται από τη μονοτονία όπως γράφει ο Τόλης παραπάνω.
και άρα από Bolzano έχουμε την ύπραξη της ρίζας. Τώρα η μοναδικότητα έρχεται από τη μονοτονία όπως γράφει ο Τόλης παραπάνω.![h(x)=2\sqrt[8]{3} h(x)=2\sqrt[8]{3}](/forum/ext/geomar/texintegr/latexrender/pictures/b08840375d9f0e98ca7cb712755c388e.png) ,
,![\displaystyle x = \pm \sqrt[8]{3} \displaystyle x = \pm \sqrt[8]{3}](/forum/ext/geomar/texintegr/latexrender/pictures/91863b978d50083a5eb8e9b7530446e0.png) και λόγω μονοτονίας δεν έχει άλλη ρίζα (η μαντεψιά που γράφει ο Μάριος).
και λόγω μονοτονίας δεν έχει άλλη ρίζα (η μαντεψιά που γράφει ο Μάριος).![+-\sqrt[8]{3} +-\sqrt[8]{3}](/forum/ext/geomar/texintegr/latexrender/pictures/6ee386b50936cda0a6234d6d4b7b8038.png) μοναδικές γιατί η συνάρτηση είναι γνησίως μονότονη στα επιμέρους διαστήματα.
μοναδικές γιατί η συνάρτηση είναι γνησίως μονότονη στα επιμέρους διαστήματα.
 και
και  .
.  και
και  . Άρα, οι
. Άρα, οι  δεν είναι ίσες. Για κάθε
δεν είναι ίσες. Για κάθε  έχουμε ότι:
έχουμε ότι:
 Άρα
Άρα  .
.  και άρα
και άρα  .
.  .
. ,
,  . Η απόσταση του
. Η απόσταση του  από την αρχή των αξόνων δίνεται από τη σχέση:
από την αρχή των αξόνων δίνεται από τη σχέση: 
 , άρα
, άρα  άρτια.
άρτια. με
με  . Τότε
. Τότε  και
και  . Άρα,
. Άρα,  . Άρα,
. Άρα, ![\left ( -\infty ,0 \right ] \left ( -\infty ,0 \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/1a80e9bfb475072dc3d68009b3d51d21.png) .
. με
με  . Άρα,
. Άρα,  .
. από το προηγούμενο ερώτημα η
από το προηγούμενο ερώτημα η ![\displaystyle h\left ( x \right )=2\sqrt[8]{3}=h\left ( \sqrt[8]{3} \right )\Leftrightarrow x=\sqrt[8]{3} \displaystyle h\left ( x \right )=2\sqrt[8]{3}=h\left ( \sqrt[8]{3} \right )\Leftrightarrow x=\sqrt[8]{3}](/forum/ext/geomar/texintegr/latexrender/pictures/96edd3d066245f1dac9a570ef888f5ad.png) .
. από το προηγούμενο ερώτημα η
από το προηγούμενο ερώτημα η ![\displaystyle h\left ( x \right )=2\sqrt[8]{3}=h\left (- \sqrt[8]{3} \right )\Leftrightarrow x=-\sqrt[8]{3} \displaystyle h\left ( x \right )=2\sqrt[8]{3}=h\left (- \sqrt[8]{3} \right )\Leftrightarrow x=-\sqrt[8]{3}](/forum/ext/geomar/texintegr/latexrender/pictures/a68713b045730e7a839692c886c94c89.png)
![\displaystyle M\left ( \sqrt[8]{3},\sqrt[8]{3^{5}} \right ) \displaystyle M\left ( \sqrt[8]{3},\sqrt[8]{3^{5}} \right )](/forum/ext/geomar/texintegr/latexrender/pictures/2ac46dfa4db39bf522f144d57815cb33.png) ή το
ή το ![\displaystyle M\left ( -\sqrt[8]{3},-\sqrt[8]{3^{5}} \right ) \displaystyle M\left ( -\sqrt[8]{3},-\sqrt[8]{3^{5}} \right )](/forum/ext/geomar/texintegr/latexrender/pictures/6256b17b80fb26982c63cf35d52900dd.png) .
.