![f:[2,8]\rightarrow \mathbb{R} f:[2,8]\rightarrow \mathbb{R}](/forum/ext/geomar/texintegr/latexrender/pictures/e12204a606237b3b95947f6a510c837a.png) με:
με:  για κάθε
για κάθε ![xε[2,8] xε[2,8]](/forum/ext/geomar/texintegr/latexrender/pictures/9112cf245d3d4d3d53b3b3abd69d4828.png)
και
 . Να αποδείξετε ότι:
. Να αποδείξετε ότι:α)
 ,
,β) υπάρχει μοναδικό
 με
με  ,
,γ) υπάρχει μοναδικό
![x2ε[2,8] x2ε[2,8]](/forum/ext/geomar/texintegr/latexrender/pictures/22b70726c8193c87907a0d1739a608e5.png) με
με  .
.Συγχωρήστε με για το γράψιμο αλλά το latex μου δεν λειτουργεί καλά.
Συντονιστής: m.pαpαgrigorakis
![f:[2,8]\rightarrow \mathbb{R} f:[2,8]\rightarrow \mathbb{R}](/forum/ext/geomar/texintegr/latexrender/pictures/e12204a606237b3b95947f6a510c837a.png) με:
με:  για κάθε
για κάθε ![xε[2,8] xε[2,8]](/forum/ext/geomar/texintegr/latexrender/pictures/9112cf245d3d4d3d53b3b3abd69d4828.png)
 . Να αποδείξετε ότι:
. Να αποδείξετε ότι: ,
, με
με  ,
,![x2ε[2,8] x2ε[2,8]](/forum/ext/geomar/texintegr/latexrender/pictures/22b70726c8193c87907a0d1739a608e5.png) με
με  .
. για κάθε
για κάθε  έχουμε ότι η
έχουμε ότι η  διατηρεί πρόσημο.
διατηρεί πρόσημο. ήταν αρνητική θα είχαμε
ήταν αρνητική θα είχαμε  το οποίο είναι άτοπο από υπόθεση.
το οποίο είναι άτοπο από υπόθεση. είναι γνησίως φθίνουσα έχουμε
είναι γνησίως φθίνουσα έχουμε  οπότε
οπότε  , οπότε
, οπότε  . Ομοίως έχουμε
. Ομοίως έχουμε  , οπότε
, οπότε  . Τώρα το θεώρημα ενδιαμέσων τιμών αποδεικνύει το β).
. Τώρα το θεώρημα ενδιαμέσων τιμών αποδεικνύει το β). δεν μηδενίζεται,τότε διατηρεί πρόσημο.
δεν μηδενίζεται,τότε διατηρεί πρόσημο. γα κάθε
γα κάθε  τότε
τότε  ,
,  και
και  .
. το οποίο είναι άτοπο.
το οποίο είναι άτοπο. για κάθε
για κάθε  τότε ομοίως θα είχαμε
τότε ομοίως θα είχαμε  , το οποίο είναι πάλι άτοπο.
, το οποίο είναι πάλι άτοπο.![x_2 \in [2,8] x_2 \in [2,8]](/forum/ext/geomar/texintegr/latexrender/pictures/ddcf14f4c2c72d1fcb33e7fa5254bdec.png) ώστε
ώστε  .
. είναι μοναδικό επειδή η συνάρτηση
είναι μοναδικό επειδή η συνάρτηση  είναι γνησίως φθίνουσα, το οποίο αποδεικνύει το γ).
είναι γνησίως φθίνουσα, το οποίο αποδεικνύει το γ).Καλησπέρα σε όλους και Χρόνια Πολλά στους εορτάζοντες.panagiotis iliopoulos έγραψε: ↑Τετ Απρ 22, 2020 6:40 amΔίνεται η συνεχής και γνησίως φθίνουσα συνάρτησημε:
για κάθε
![xε[2,8] xε[2,8]](/forum/ext/geomar/texintegr/latexrender/pictures/9112cf245d3d4d3d53b3b3abd69d4828.png)
και. Να αποδείξετε ότι:
α),
β) υπάρχει μοναδικόμε
,
γ) υπάρχει μοναδικόμε
.
Συγχωρήστε με για το γράψιμο αλλά το latex μου δεν λειτουργεί καλά.
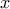 και ότι είναι
και ότι είναι 
 ως συνεχής θα διατηρεί το πρόσημο της
ως συνεχής θα διατηρεί το πρόσημο της 
 καθώς και παίρνοντας όρια ,
καθώς και παίρνοντας όρια ,
 το οποίο είναι Άτοπο.
το οποίο είναι Άτοπο.Είναι ακριβώς η ίδια λύση με τη δικιά μου παραπάνω. Νομίζω δεν υπάρχει λόγος να γράφουμε τα ίδια πράγματα.Άρχοντας έγραψε: ↑Πέμ Απρ 23, 2020 11:36 pmΑ) Επειδή η f δεν μηδενίζεται στο διάστημα [2,8] και f συνεχής στο [2,8] τότε η f διατηρεί σταθερό πρόσημο. Αν η f(x)<0 τότε f(2)f(4)f(8)<0 άτοπο διότι f(2)f(4)f(8)=64>0 Β) 2<4<8 επειδή f γνησίως φθίνουσα άρα f(2)>f(4)>f(8). Επίσης f(2)>f(4) και f(2)>f(8) πολλαπλασιάζοντας κατά μέλη θα πάρουμε f(2)f(2)>f(4)f(8) και τέλος πολλαπλασιάζοντας με f(2) και τα δύο μέλη παίρνουμε ότι f³(2)>f(2)f(4)f(8)=64 τέλος f(2)>4. Επιπλέον f(8)<f(2) και f(8)<f(4) πολλαπλασιάζοντας κατά μέλη έχουμε ότι f(8)f(8)<f(2)f(4) και πολλαπλασιάζοντας με f(8) παίρνουμε f³(8)<f(2)f(4)f(8)=64 και τελικά f(8)<4. Τέλος από ΘΕΤ υπάρχει τουλάχιστον ένα x1ε(2,8):f(x1)=4 και επειδή f γνησίως φθίνουσα το χ1 είναι μοναδικό. Γ) θεωρώ συνάρτηση g(x)=f(x)-x αν g(x)>0 τότε και f(x)-x>0 άρα f(x)>x αν x=2 τότε f(2)>2 αν x=4 τότε f(4)>4 αν x=8 τότε f(8)>8 και πολλαπλασιάζοντας κατά μέλη παίρνουμε ότι f(2)f(4)f(8)>64 άτοπο ομοίως και για g(x)<0 επομένως υπάρχει x2ε[2,8]:g(x2)=0 ή f(x2)=x2 και επειδή g γνησίως φθίνουσα το x2 είναι μοναδικό. Τέλος ζητώ ταπεινά συγγνώμη που δεν γράφω σε latex αλλά είμαι νέο μέλος και δεν έχω μάθει ακόμα να γράφω σε latex. Καλό βράδυ.
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες