 με πεδίο ορισμού το
με πεδίο ορισμού το  για την οποία ισχύει ότι :
για την οποία ισχύει ότι :  για κάθε
για κάθε  . Πως μπορεί ένας μαθητής βασιζόμενος στο σχολικό βιβλίο να δικαιολογήσει επαρκώς ότι το σύνολο τιμών της
. Πως μπορεί ένας μαθητής βασιζόμενος στο σχολικό βιβλίο να δικαιολογήσει επαρκώς ότι το σύνολο τιμών της  , είναι το
, είναι το  ;
;Συντονιστής: m.pαpαgrigorakis
 με πεδίο ορισμού το
με πεδίο ορισμού το  για την οποία ισχύει ότι :
για την οποία ισχύει ότι :  για κάθε
για κάθε  . Πως μπορεί ένας μαθητής βασιζόμενος στο σχολικό βιβλίο να δικαιολογήσει επαρκώς ότι το σύνολο τιμών της
. Πως μπορεί ένας μαθητής βασιζόμενος στο σχολικό βιβλίο να δικαιολογήσει επαρκώς ότι το σύνολο τιμών της  , είναι το
, είναι το  ;
;Από την υπόθεση είναι
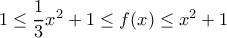 με ισότητα αν
με ισότητα αν  , οπότε ελάχιστη τιμή το
, οπότε ελάχιστη τιμή το 
 επιλέγουμε
επιλέγουμε 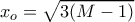 (βασικά λύσαμε την
(βασικά λύσαμε την 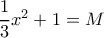 ). Είναι τότε
). Είναι τότε  , Άρα από συνέχεια το
, Άρα από συνέχεια το  είναι στο σύνολο τιμών της
είναι στο σύνολο τιμών της  .
. , έπεται ότι
, έπεται ότι  . Θέτοντας όπου
. Θέτοντας όπου  το
το  στη δοσμένη ανισότητα έπεται ότι
στη δοσμένη ανισότητα έπεται ότι  , οπότε
, οπότε  και έτσι
και έτσι  , άρα η
, άρα η  παρουσιάζει ολικό ελάχιστο στο
παρουσιάζει ολικό ελάχιστο στο  το
το  .
. . Έπειτα, παίρνουμε
. Έπειτα, παίρνουμε  , οπότε βρίσκουμε
, οπότε βρίσκουμε  κοντά στο
κοντά στο  με
με  και κάνουμε Θ.Ε.Τ. στο
και κάνουμε Θ.Ε.Τ. στο ![[0,a] [0,a]](/forum/ext/geomar/texintegr/latexrender/pictures/13596d6674a86fdafa24c4c414033e58.png) .
. . Θεωρούμε την εξίσωση:
. Θεωρούμε την εξίσωση:

![[0,\sqrt{3\eta}] [0,\sqrt{3\eta}]](/forum/ext/geomar/texintegr/latexrender/pictures/e51f3127c069df3b521bba4bf1ede4df.png) και έχουμε
και έχουμε  τέτοιο ώστε
τέτοιο ώστε  .
.  και
και  , έπεται ότι
, έπεται ότι  .
.
 και
και 

 ενός διαστήματος
ενός διαστήματος  μέσω μιας συνεχούς και μη σταθερής
μέσω μιας συνεχούς και μη σταθερής  είναι διάστημα.''
είναι διάστημα.''
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 12 επισκέπτες