 , με
, με και
και  .
.Να αποδείξετε ότι :
i. υπάρχει
 τέτοιο, ώστε
τέτοιο, ώστε 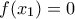 .
.ii. υπάρχει
 τέτοιο, ώστε
τέτοιο, ώστε  .
.iii. υπάρχει
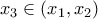 τέτοιο, ώστε
τέτοιο, ώστε  .
.Συντονιστής: m.pαpαgrigorakis
 , με
, με και
και  .
. τέτοιο, ώστε
τέτοιο, ώστε 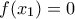 .
. τέτοιο, ώστε
τέτοιο, ώστε  .
.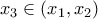 τέτοιο, ώστε
τέτοιο, ώστε  .
. είναι συνεχείς ως πολυωνυμικές συναρτήσεις
είναι συνεχείς ως πολυωνυμικές συναρτήσεις 

 είναι συνεχής στο κλειστό διάστημα
είναι συνεχής στο κλειστό διάστημα ![[1,2] [1,2]](/forum/ext/geomar/texintegr/latexrender/pictures/f79408e5ca998cd53faf44af31e6eb45.png) με
με  και
και  , άρα σύμφωνα με το θ. Bolzano υπάρχει τουλάχιστον ένα
, άρα σύμφωνα με το θ. Bolzano υπάρχει τουλάχιστον ένα 
 είναι συνεχής στο κλειστό διάστημα
είναι συνεχής στο κλειστό διάστημα ![[2,3] [2,3]](/forum/ext/geomar/texintegr/latexrender/pictures/d5138fec13c27bb6c645b29cdfa97a84.png) με
με  και
και  , άρα σύμφωνα με το θ. Bolzano υπάρχει τουλάχιστον ένα
, άρα σύμφωνα με το θ. Bolzano υπάρχει τουλάχιστον ένα 
 οδηγεί στην εύρεση ρίζας εντός του διαστήματος
οδηγεί στην εύρεση ρίζας εντός του διαστήματος  της συνεχούς ως πολυωνυμικής
της συνεχούς ως πολυωνυμικής  , με τύπο
, με τύπο 
 και αφού η
και αφού η 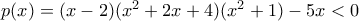 για
για  ως άθροισμα αρνητικών ποσοτήτων , αναζητούμε το πρόσήμο της για
ως άθροισμα αρνητικών ποσοτήτων , αναζητούμε το πρόσήμο της για  όπου
όπου  καθώς
καθώς  . H
. H  με
με  , τότε
, τότε 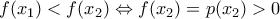

 αλλά δεν είχα σαφαλή συμπεράσματα. Τώρα αν κάποιος έχει ιδέα για το αν θα βοηθήσουν με χαρά μου να τη δω. Ευχαριστώ
αλλά δεν είχα σαφαλή συμπεράσματα. Τώρα αν κάποιος έχει ιδέα για το αν θα βοηθήσουν με χαρά μου να τη δω. Ευχαριστώ το ΘΒ δίνει
το ΘΒ δίνει 
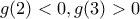 το ΘΒ δίνει
το ΘΒ δίνει 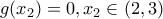


 με ΘΒ το ζητούμενο
με ΘΒ το ζητούμενο άρα
άρα θα δείξω ότι
θα δείξω ότι  η
η 
 τοτε
τοτε  συνεπώς
συνεπώς  Άτοπο αφού
Άτοπο αφού 
 βρίσκεται άνωθεν της εφαπτομένης στο
βρίσκεται άνωθεν της εφαπτομένης στο  που έχει θετικές τεταγμένες για
που έχει θετικές τεταγμένες για  άρα
άρα 

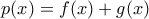 στο διάστημα
στο διάστημα ![[x_{1},x_{2}] [x_{1},x_{2}]](/forum/ext/geomar/texintegr/latexrender/pictures/48f0a3fbaaf45d915fd69980c25b8d48.png) (αρκετά εύκολο αυτό), υπάρχει λοιπόν
(αρκετά εύκολο αυτό), υπάρχει λοιπόν 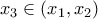 , ώστε
, ώστε  , υποθέτουμε ότι
, υποθέτουμε ότι  , άρα και
, άρα και  , που καταλήγει σε άτοπο.
, που καταλήγει σε άτοπο. , παίρνουμε το ζητούμενο.
, παίρνουμε το ζητούμενο.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες