 ισχύει
ισχύει 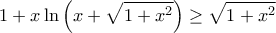
Συντονιστής: m.pαpαgrigorakis
 ισχύει
ισχύει 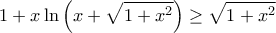

Καλησπέρα. Μια προσπάθεια ...
 , 2φορές παραγωγίσιμη με
, 2φορές παραγωγίσιμη με και
και  .
. για κάθε
για κάθε  , συνεπώς η
, συνεπώς η  είναι γνησίως αύξουσα.
είναι γνησίως αύξουσα. . Άρα
. Άρα 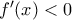 για κάθε
για κάθε  , επομένως η η
, επομένως η η  είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο ![(-\infty , 0 ] (-\infty , 0 ]](/forum/ext/geomar/texintegr/latexrender/pictures/ae4b858aa3a823bc1fa516f89f5a573d.png) .
. για κάθε
για κάθε 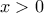 , επομένως η η
, επομένως η η  είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο  .
. παρουσιάζει ολικό ελάχιστο στο
παρουσιάζει ολικό ελάχιστο στο  το
το  .
.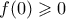

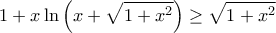
 η ανισότητα γίνεται
η ανισότητα γίνεται  .
.  είναι άρτια και ισχύει
είναι άρτια και ισχύει  καθώς και
καθώς και  . Η παράγωγος είναι ομόσημη του
. Η παράγωγος είναι ομόσημη του  οπότε το
οπότε το  είναι ολικό ελάχιστο.
είναι ολικό ελάχιστο.Έστω
 με
με  ,
, πάντα.
πάντα. στρέφει άνω τα κοίλα στο
στρέφει άνω τα κοίλα στο  και αφού έχει εφαπτομένη στο
και αφού έχει εφαπτομένη στο  την ευθεία με εξίσωση
την ευθεία με εξίσωση  για κάθε
για κάθε  ,
, 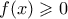 .
.Με ολοκληρώματα.
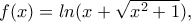 και
και 


 είναι
είναι  και επειδή
και επειδή  ολοκληρώνοντας παίρνουμε την ζητούμενη.
ολοκληρώνοντας παίρνουμε την ζητούμενη. μπορεί να όρισθεί στο
μπορεί να όρισθεί στο  ώστε να είναι συνεχής)
ώστε να είναι συνεχής) πάλι είναι
πάλι είναι  .
. .
. και πολλαπλασιάζοντας με
και πολλαπλασιάζοντας με  παίρνουμε την ζητούμενη.
παίρνουμε την ζητούμενη.Γεια σου Γιώργο.
 πρέπει να έχουμε ανισότητα για
πρέπει να έχουμε ανισότητα για 
![lnx=\lim_{n\rightarrow \infty }n(\sqrt[n]{x}-1) lnx=\lim_{n\rightarrow \infty }n(\sqrt[n]{x}-1)](/forum/ext/geomar/texintegr/latexrender/pictures/6fd99b560bdedb366839ed19e73b85ca.png)

 και την δεξιά για
και την δεξιά για  βγαίνει.
βγαίνει.Για
 το παραπάνω ισχύει ως ισότητα. Για
το παραπάνω ισχύει ως ισότητα. Για  αρκεί να δειχθεί ότι:
αρκεί να δειχθεί ότι:
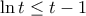 με
με 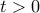 θέτουμε
θέτουμε  και έχουμε:
και έχουμε: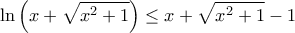
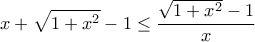 . Πράγματι , έχουμε:
. Πράγματι , έχουμε:
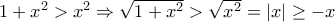 .
. αρκεί να δειχθεί
αρκεί να δειχθεί  . Είναι
. Είναι  για κάθε
για κάθε  . Άρα
. Άρα  . Αν
. Αν 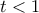 είναι
είναι  . Αφού για
. Αφού για  είναι:
είναι: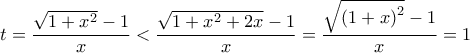
 και αρκεί να δειχθεί ότι
και αρκεί να δειχθεί ότι  το οποίο ισχύει αφού ισοδυναμεί με
το οποίο ισχύει αφού ισοδυναμεί με  .
.

Υπόδειξη: Για ευκολία άλλαξε το όνομα της μεταβλητής (παρακάτω θα καταλάβεις γιατί (*)) και ζήτα το
![\log a=\lim \limits_{n\rightarrow +\infty }n(\sqrt[n]{a}-1) \log a=\lim \limits_{n\rightarrow +\infty }n(\sqrt[n]{a}-1)](/forum/ext/geomar/texintegr/latexrender/pictures/e8cc2c2fca85f41a07e4bbc0510db42b.png) .
. ή ακόμα καλύτερα
ή ακόμα καλύτερα 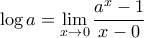 . Συσχέτισε το τελευταίο με την παράγωγο του
. Συσχέτισε το τελευταίο με την παράγωγο του  στο
στο  .
. . Αν δεν αλλάζαμε το όνομα της μεταβλητής θα ψάχναμε την παράγωγο ως προς
. Αν δεν αλλάζαμε το όνομα της μεταβλητής θα ψάχναμε την παράγωγο ως προς  της
της 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες