-Αν υπάρχει το
 αλλά όχι το
αλλά όχι το  , τότε δεν υπάρχει και το
, τότε δεν υπάρχει και το 
Εγώ νομίζω ότι πρέπει να προσθέσει και κάτι ακόμα στην πρόταση αυτή ο καθηγητής. Να εξηγήσω γιατί.
Θέτω
 άρα
άρα  και έστω ότι το όριο της
και έστω ότι το όριο της  υπάρχει. Τότε, αφού υπάρχει το όριο της
υπάρχει. Τότε, αφού υπάρχει το όριο της  θα υπάρχει και το όριο της
θα υπάρχει και το όριο της  . ΑΤΟΠΟ, άρα Σωστό.
. ΑΤΟΠΟ, άρα Σωστό.Όμως, αν π.χ. πάρω το
 και το
και το  , τότε ενώ το πρώτο όριο δεν υπάρχει και το δεύτερο υπάρχει, το όριο του αθροίσματος υπάρχει.
, τότε ενώ το πρώτο όριο δεν υπάρχει και το δεύτερο υπάρχει, το όριο του αθροίσματος υπάρχει.
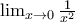 δεν υπάρχει αλλά
δεν υπάρχει αλλά  .
. για
για 
 για
για 
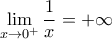 και
και 
 είναι φραγμένη, οπότε τελικά το άθροισμά τους έχει όριο
είναι φραγμένη, οπότε τελικά το άθροισμά τους έχει όριο 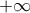 στο
στο  και
και  στο
στο 
 αλλά σε αυτό το σκέλος απάντησες ορθότατα. Μένει όμως η ουσία).
αλλά σε αυτό το σκέλος απάντησες ορθότατα. Μένει όμως η ουσία).  και
και  είναι "συν άπειρο" (απλό και ουσιαστικά το έκανες) αλλά της
είναι "συν άπειρο" (απλό και ουσιαστικά το έκανες) αλλά της  δεν υπάρχει (
δεν υπάρχει (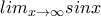 δε ξέρουμε την τιμή του αλλά ξέρουμε ότι θα είναι κάπου ανάμεσα στο
δε ξέρουμε την τιμή του αλλά ξέρουμε ότι θα είναι κάπου ανάμεσα στο  και
και  οπότε αφού το
οπότε αφού το 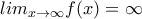 , τότε θα στέλνει και το άθροισμα των συναρτήσεων στο άπειρο.
, τότε θα στέλνει και το άθροισμα των συναρτήσεων στο άπειρο.  δεν υπάρχει.
δεν υπάρχει.
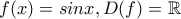

 ,
, 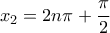 ,
,  .
.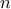 αυξάνεται στους φυσικούς αριθμούς, οι πραγματικοί αριθμοί
αυξάνεται στους φυσικούς αριθμούς, οι πραγματικοί αριθμοί  πάνε σε οποιονδήποτε μεγάλο θετικό πραγματικό θέλουμε, άρα
πάνε σε οποιονδήποτε μεγάλο θετικό πραγματικό θέλουμε, άρα 
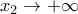 . Όμως:
. Όμως: ενώ
ενώ 