ΑΣΚΗΣΗ
Να αποδείξετε ότι κάθε συνάρτηση
 με την ιδιότητα
με την ιδιότητα  ,
,  είναι
είναι 
Συντονιστής: m.pαpαgrigorakis
 με την ιδιότητα
με την ιδιότητα  ,
,  είναι
είναι 
 για κάθε
για κάθε 
 τέτοιος, ώστε
τέτοιος, ώστε  Τότε, θα είχαμε ότι:
Τότε, θα είχαμε ότι:
 τέτοιος, ώστε
τέτοιος, ώστε  τότε θα είχαμε ότι:
τότε θα είχαμε ότι:
 και
και  ισχύει ότι το
ισχύει ότι το  είναι μονοσύνολο για
είναι μονοσύνολο για  . Αφού προφανώς
. Αφού προφανώς  παίρνουμε
παίρνουμε 
Βαγγέλη, αναρωτήθηκα αν μπορούμε να βρούμε τον τύπο της f (στην αρχική έκδοση η άσκηση είχε και ένα -2 στο τέλος της εκφώνησες και το έσβησα), αλλά δεν το επιχείρησα.Σκόπευα μάλιστα να εξετάσω μήπως να την έδινα παραγωγίσιμη, ώστε να γίνει πιο εύκολη. Σε ευχαριστώ πολύ που με γλύτωσες από ...μπελάδες και κάμποσο χρόνο !!!!emouroukos έγραψε: ↑Πέμ Νοέμ 16, 2017 3:27 pmΘα αποδείξουμε ότιγια κάθε
Έστω ότι υπήρχετέτοιος, ώστε
Τότε, θα είχαμε ότι:
που είναι άτοπο. Όμοια, αν υπήρχετέτοιος, ώστε
τότε θα είχαμε ότι:
πάλι άτοπο.
 για κάθε
για κάθε  .
.  , οπότε αν για κάποιο
, οπότε αν για κάποιο  ισχύει
ισχύει  , τότε
, τότε 
 ανάμεσα στα
ανάμεσα στα  ώστε το αριστερό μέλος να ισούται με
ώστε το αριστερό μέλος να ισούται με  , άτοπο.
, άτοπο.πως γνωρίζουμε ότι η
 είναι αντιστρέψιμη για κάθε
είναι αντιστρέψιμη για κάθε  ; Δημήτρη ,μπορείς λίγο να εξηγήσεις λίγο αναλυτικότερα την σκέψη σου; Ευχαριστώ εκ των προτέρων !
; Δημήτρη ,μπορείς λίγο να εξηγήσεις λίγο αναλυτικότερα την σκέψη σου; Ευχαριστώ εκ των προτέρων ! είναι συνεχής και κυρτή.
είναι συνεχής και κυρτή.  , με το
, με το  αναφέρομαι απλώς στο σύνολο των αριθμών
αναφέρομαι απλώς στο σύνολο των αριθμών  με
με  ).
). και
και  , ενώ
, ενώ  .
.  (
( < 0) και μοναδική ρίζα
< 0) και μοναδική ρίζα  . Είναι γνησίως φθίνουσα στο
. Είναι γνησίως φθίνουσα στο  με
με  για
για  και γνησίως αύξουσα στο
και γνησίως αύξουσα στο  με
με  για
για  . Έτσι προκύπτει το ζητούμενο.
. Έτσι προκύπτει το ζητούμενο.


 η οποία είναι γνησίως αύξουσα στο
η οποία είναι γνησίως αύξουσα στο  άρα και
άρα και 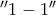 με
με 
 γράφεται:
γράφεται:
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης