Σωστό - Λάθος στη συνέχεια

nik21 · #1

Δίνεται $f:\mathbb{R}\to \mathbb{R}$

Η

είναι συνεχής στο $\displaystyle{ x_0 }\in R} \Leftrightarrow\displaystyle{\underset{f(x)\to f(x_0)}{\mathop{\lim }}x\,}}=\displaystyle{ x_0 }$

Μου ήρθε ως ιδέα για Σ-Λ λύνοντας μια αντίστοιχη άσκηση.

Christos.N · #2

Εύκολα σαν αντιπαράδειγμα έχουμε το όριο

$\displaystyle{ \mathop {\lim x}\limits_{x^2 \to 1} = 1 }$
όπου $\displaystyle{ f(x) = x^2 }$

slash · #3

Νομίζω θα ήταν σωστό αν έλεγε και 1-1.

nik21 · #4

Ευχαριστώ και τους δύο για την ενασχόληση.

Από το παρακάτω προέκυψε η ιδέα:

slash έγραψε:Νομίζω θα ήταν σωστό αν έλεγε και 1-1.

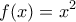
στην προσπάθειά μου να κάνω μια απόδειξη της συνέχειας της αντίστροφης μιας συνεχούς στο

συνάρτησης, κατανοητή σε μαθητές Γ Λυκείου.
Θα την αναφέρω κάποια στιγμή που θα έχω χρόνο γιατι οι γνώσεις μου στο LaTeX είναι του νηπιαγωγείου

#5

nik21 έγραψε:Δίνεται $f:\mathbb{R}\to \mathbb{R}$

Η είναι συνεχής στο $\displaystyle{ x_0 }\in R} \Leftrightarrow\displaystyle{\underset{f(x)\to f(x_0)}{\mathop{\lim }}x\,}}=\displaystyle{ x_0 }$

Μου ήρθε ως ιδέα για Σ-Λ λύνοντας μια αντίστοιχη άσκηση.

Δεν νομίζω να έχει δοθεί ορισμός για το $\displaystyle{ \lim_{f(x) \to f(x_0)}x}$ .

Σωστό - Λάθος στη συνέχεια

Σωστό - Λάθος στη συνέχεια

Re: Σωστό - Λάθος στη συνέχεια

Re: Σωστό - Λάθος στη συνέχεια

Re: Σωστό - Λάθος στη συνέχεια

Re: Σωστό - Λάθος στη συνέχεια

Μέλη σε σύνδεση