 συνάρτηση
συνάρτηση  για την οποία ισχύουν οι σχέσεις
για την οποία ισχύουν οι σχέσεις για κάθε
για κάθε  και
και 
Α. Να δειχθεί ότι

B.Aν
 συνεχής στο
συνεχής στο 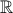 , Tότε
, Tότε 
Γ.Να δείξετε ότι

Δ. Αν η εξίσωση
 , έχει μοναδική ρίζα το
, έχει μοναδική ρίζα το  , τότε η
, τότε η  αντιστρέφεται και ισχύει
αντιστρέφεται και ισχύει 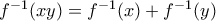
Συντονιστής: m.pαpαgrigorakis
 συνάρτηση
συνάρτηση  για την οποία ισχύουν οι σχέσεις
για την οποία ισχύουν οι σχέσεις για κάθε
για κάθε  και
και 

 συνεχής στο
συνεχής στο 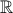 , Tότε
, Tότε 

 , έχει μοναδική ρίζα το
, έχει μοναδική ρίζα το  , τότε η
, τότε η  αντιστρέφεται και ισχύει
αντιστρέφεται και ισχύει 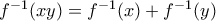
 οπότε για
οπότε για  έχουμε
έχουμε  διότι
διότι  αφού
αφού  για κάθε
για κάθε 
 με
με 
 . Επειδή η f είναι συνεχής απο θεώρημα Bolzano έχω οτι υπάρχει
. Επειδή η f είναι συνεχής απο θεώρημα Bolzano έχω οτι υπάρχει  τέτοιο ώστε
τέτοιο ώστε  ΑΤΟΠΟ,διότι
ΑΤΟΠΟ,διότι  για κάθε
για κάθε 

 έχουμε
έχουμε 
 με
με  οπότε η f είναι 1-1,επομένως αντιτρέφεται.
οπότε η f είναι 1-1,επομένως αντιτρέφεται. και
και 



Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 10 επισκέπτες