Εστω

μη μηδενικοί μιγαδικοί.
Οι διανυσματικές ακτίνες τους είναι κάθετες αν και μόνο αν ο ένας προκύπτει από τον άλλο με στροφή κατά

Δηλαδή

i)Εχουμε ότι

Αρκεί να δείξουμε ότι οι
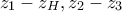
είναι κάθετοι.
(ταυτίζω τις διανυσματικές ακτίνες με τους μιγαδικούς στα επόμενα)
Δηλαδή

Ισχύει γιατί το

είναι ισο με

ii)Εστω

οι μιγαδικοί που είναι οι κορυφές του τετραπλεύρου.
Μπορούμε να υποθέσουμε οτι το κέντρο του περιγεγράμενου κύκλου είναι το

Τα ορθόκεντρα είναι οι μιγαδικοί

Παρατηρούμε ότι

και όμοια για τα άλλα.
Το τετράπλευρο που σχηματίζουν τα ορθόκεντρα έχει ίσες πλευρές με το αρχικό.
Επίσης είναι εγγεγραμένο σε κύκλο ίδιας ακτίνας με τον αρχικό και κέντρο το

Αρα είναι ίσα
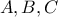 οι αντίστοιχες εικόνες των μιγαδικών σχηματίζουν τρίγωνο του οποίου το περίκεντρο αντιστοιχει στην αρχή των αξόνων ,τότε να δείξετε ότι το ορθόκεντρο
οι αντίστοιχες εικόνες των μιγαδικών σχηματίζουν τρίγωνο του οποίου το περίκεντρο αντιστοιχει στην αρχή των αξόνων ,τότε να δείξετε ότι το ορθόκεντρο  του τριγώνου αντιστοιχεί στον μιγαδικό :
του τριγώνου αντιστοιχεί στον μιγαδικό : 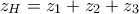
 εγγράψιμμο τετράπλευρο και
εγγράψιμμο τετράπλευρο και  τα ορθόκεντρα των τριγώνων
τα ορθόκεντρα των τριγώνων 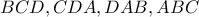 αντιστοίχως,
αντιστοίχως, είναι ίσο με το τετράπλευρο
είναι ίσο με το τετράπλευρο 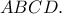

 μη μηδενικοί μιγαδικοί.
μη μηδενικοί μιγαδικοί.


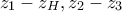 είναι κάθετοι.
είναι κάθετοι.
 είναι ισο με
είναι ισο με 
 οι μιγαδικοί που είναι οι κορυφές του τετραπλεύρου.
οι μιγαδικοί που είναι οι κορυφές του τετραπλεύρου.

 και όμοια για τα άλλα.
και όμοια για τα άλλα. 