Καλησπέρα. Ωραίο!
Μια λύση λίγο διαφορετική από του κ.Μιχάλη και εκτός ύλης Λυκείου
(!)
Η μια κατεύθυνση είναι άμεση από την τριγωνική ανισότητα.
Για την άλλη κατεύθυνση, θα λύναμε το πρόβλημα άμεσα αν βρίσκαμε

με

τέτοιο ώστε

. Βρίσκουμε

τέτοιο ώστε

. Τέτοιο

υπάρχει διότι το δεξί μέλος έχει μέτρο

. Χρησιμοποιούμε το

. Αυτό δουλεύει στην

:
 (!) Με την παρατήρηση του κ.Μιχάλη παρακάτω, θυμήθηκα ότι ο ορισμός του
(!) Με την παρατήρηση του κ.Μιχάλη παρακάτω, θυμήθηκα ότι ο ορισμός του  είναι εκτός ύλης Λυκείου. Με συγχωρείτε, έχουν περάσει χρόνια.
είναι εκτός ύλης Λυκείου. Με συγχωρείτε, έχουν περάσει χρόνια. 
τελευταία επεξεργασία από
AlexandrosG σε Τρί Απρ 12, 2016 10:52 pm, έχει επεξεργασθεί 1 φορά συνολικά.
 είναι μιγαδικοί αριθμοί να αποδείξετε ότι
είναι μιγαδικοί αριθμοί να αποδείξετε ότι  για κάθε
για κάθε  με
με  αν και μόνο αν
αν και μόνο αν 
 δεν ήταν ακέραιος όπως εκ παραδρομής γράφτηκε αλλά μιγαδικός. Ευχαριστώ τον Γιάννη Σταματογιάννη για την υπόδειξη!
δεν ήταν ακέραιος όπως εκ παραδρομής γράφτηκε αλλά μιγαδικός. Ευχαριστώ τον Γιάννη Σταματογιάννη για την υπόδειξη!
 με
με  Για οποιοδήποτε
Για οποιοδήποτε  , όπως θέλαμε.
, όπως θέλαμε. Γράφουμε
Γράφουμε  (τριγωνομετρική μορφή μιγαδικών) και επιλέγουμε
(τριγωνομετρική μορφή μιγαδικών) και επιλέγουμε  , οπότε
, οπότε  .
. έχουμε
έχουμε 


 . Βρίσκουμε
. Βρίσκουμε  τέτοιο ώστε
τέτοιο ώστε  . Τέτοιο
. Τέτοιο  . Χρησιμοποιούμε το
. Χρησιμοποιούμε το  . Αυτό δουλεύει στην
. Αυτό δουλεύει στην  :
:
 είναι εκτός ύλης Λυκείου. Με συγχωρείτε, έχουν περάσει χρόνια.
είναι εκτός ύλης Λυκείου. Με συγχωρείτε, έχουν περάσει χρόνια. 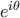 και τα παρόμοια γιατί είμαστε σε φάκελο Λυκείου.
και τα παρόμοια γιατί είμαστε σε φάκελο Λυκείου.  που έγραψα, καθώς και τα παρεμφερή, με το
που έγραψα, καθώς και τα παρεμφερή, με το