 με
με 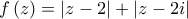 ,
,όπου
 .
.Ν.Ζ.
Συντονιστής: Πρωτοπαπάς Λευτέρης
 με
με 

 έχουμε
έχουμε


 η τιμή
η τιμή  είναι το ζητούμενο μέγιστο.
είναι το ζητούμενο μέγιστο.Καλημέρα Νίκο!nikoszan έγραψε:Να βρείτε την μέγιστη τιμή της συνάρτησηςμε
,
όπου.
Ν.Ζ.

 \displaystyle{\displaystyle{\mathop \le \limits^{C - S} \sqrt 2 \sqrt {10 - 4\left( {x + y} \right)} }
\displaystyle{\displaystyle{\mathop \le \limits^{C - S} \sqrt 2 \sqrt {10 - 4\left( {x + y} \right)} } \displaystyle{x = \cos a,y = \sin a,a \in [0,2\pi )}
\displaystyle{x = \cos a,y = \sin a,a \in [0,2\pi )} \displaystyle{x + y = \cos a + \sin a = \sqrt 2 \cos \left( {\frac{\pi }{4} - a} \right) \Rightarrow - \sqrt 2 \le x + y \le \sqrt 2 \Leftrightarrow ....10 - 4\sqrt 2 \le 10 - 4\left( {x + y} \right) \le 10 + 4\sqrt 2 }}
\displaystyle{x + y = \cos a + \sin a = \sqrt 2 \cos \left( {\frac{\pi }{4} - a} \right) \Rightarrow - \sqrt 2 \le x + y \le \sqrt 2 \Leftrightarrow ....10 - 4\sqrt 2 \le 10 - 4\left( {x + y} \right) \le 10 + 4\sqrt 2 }}

 η οποία λαμβάνεται όταν
η οποία λαμβάνεται όταν  δηλαδή για τον μιγαδικό
δηλαδή για τον μιγαδικό  και επειδή χρησιμοποιήθηκε εμβόλιμα όταν
και επειδή χρησιμοποιήθηκε εμβόλιμα όταν 
 είναι τα σημεία
είναι τα σημεία  , αντίστοιχα. Η παράσταση
, αντίστοιχα. Η παράσταση  είναι το μήκος της γραμμής
είναι το μήκος της γραμμής  (κόκκινη στο σχήμα) καθώς το
(κόκκινη στο σχήμα) καθώς το  διατρέχει τον σημειωμένο μοναδιαίο κύκλο. Στο σχήμα το
διατρέχει τον σημειωμένο μοναδιαίο κύκλο. Στο σχήμα το  έχει ληφθεί στην θέση του ζητούμενου μεγίστου (και το
έχει ληφθεί στην θέση του ζητούμενου μεγίστου (και το  είναι η αντίστοιχη του ελαχίστου). Εύκολα βλέπουμε ότι το
είναι η αντίστοιχη του ελαχίστου). Εύκολα βλέπουμε ότι το  είναι το
είναι το  , όπως πριν.
, όπως πριν. Καλησπέρα σας!Mihalis_Lambrou έγραψε:Ας δούμε και γεωμετρικό επιχείρημα που ερμηνεύει το συμπέρασμα στο οποίο κατέληξαν οι δύο προηγούμενες λύσεις. Δεν άνω τις λεπτομέρειες αλλά είναι απλό να τις συμπληρώσει κανείς.
Ταείναι τα σημεία
, αντίστοιχα. Η παράσταση
είναι το μήκος της γραμμής
(κόκκινη στο σχήμα) καθώς το
διατρέχει τον σημειωμένο μοναδιαίο κύκλο. Στο σχήμα το
έχει ληφθεί στην θέση του ζητούμενου μεγίστου (και το
είναι η αντίστοιχη του ελαχίστου). Εύκολα βλέπουμε ότι το
είναι το
, όπως πριν.
Φιλικά,
Μιχάλης
 να μεγιστοποιεί την συνάρτηση; Το μυαλό μου πήγε στην τριγωνική ανίσωση και σε αναφορές στα αντίστοιχα ημιεπίπεδα που ορίζει η
να μεγιστοποιεί την συνάρτηση; Το μυαλό μου πήγε στην τριγωνική ανίσωση και σε αναφορές στα αντίστοιχα ημιεπίπεδα που ορίζει η  , αλλά δεν έχω κάτι ικανοποιητικό.
, αλλά δεν έχω κάτι ικανοποιητικό.Θεωρούμε την έλλειψη με εστίες ταGrosrouvre έγραψε: Θα με ενδιέφερε πάρα πολύ το να δω τις λεπτομέρειες που παραλείψατε.
 και σταθερό
και σταθερό  (γαλάζια στο σχήμα). Αυτή εφάπτεται του μικρού κύκλου (γιατί έχουν κοινή εφαπτομένη).
(γαλάζια στο σχήμα). Αυτή εφάπτεται του μικρού κύκλου (γιατί έχουν κοινή εφαπτομένη).  του κύκλου έχουμε
του κύκλου έχουμε  , όπως θέλαμε.
, όπως θέλαμε. 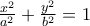 και o κύκλος
και o κύκλος  με
με  . Λύνοντας θα βρούμε κοινό σημείο μόνο το
. Λύνοντας θα βρούμε κοινό σημείο μόνο το  . Δηλαδή δεν έχουν άλλο κοινό σημείο πέραν του προφανούς, όπως θέλαμε. Λεπτομερέστερα, η πρώτη εξίσωση δίνει
. Δηλαδή δεν έχουν άλλο κοινό σημείο πέραν του προφανούς, όπως θέλαμε. Λεπτομερέστερα, η πρώτη εξίσωση δίνει  . Αφαιρώντας τις δύο εξισώσεις αφού πρώτα πολλαπλασιάσουμε την πρώτη επί
. Αφαιρώντας τις δύο εξισώσεις αφού πρώτα πολλαπλασιάσουμε την πρώτη επί  έχουμε
έχουμε  , άρα
, άρα  οπότε
οπότε  , και άρα
, και άρα  .
.
 το μέσο του τμήματος
το μέσο του τμήματος  από το θέωρημα διαμέσων θα έχουμε
από το θέωρημα διαμέσων θα έχουμε
 σταθερό αρκεί να μεγιστοποιήσουμε το ευθύγραμμο τμήμα
σταθερό αρκεί να μεγιστοποιήσουμε το ευθύγραμμο τμήμα  το οποίο μεγιστοποιείται όταν η ευθεία που ορίζει είναι διάμετρος.
το οποίο μεγιστοποιείται όταν η ευθεία που ορίζει είναι διάμετρος. .
. , οπότε με αντικατάσταση καταλήγουμε στο ίδιο πρόβλημα που έθεσε ο Νίκος. Το μόνο που θα είχαμε να δούμε είναι το max της
, οπότε με αντικατάσταση καταλήγουμε στο ίδιο πρόβλημα που έθεσε ο Νίκος. Το μόνο που θα είχαμε να δούμε είναι το max της  το οποίο πιάνεται στο 5π/4 (όλα μέσα στο απόλυτο αρνητικά άρα αυξάνουν την τιμή).
το οποίο πιάνεται στο 5π/4 (όλα μέσα στο απόλυτο αρνητικά άρα αυξάνουν την τιμή).Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 9 επισκέπτες