Συγχωρέστε μου μια τελευταία παρένθεση στους μιγαδικούς ... μια και βγήκαν εκτός ύλης!
1. Να λυθεί η εξίσωση:
 (1), με
(1), με  .
.2. Αν τα σημεία Μ,Ν είναι εικόνες των ριζών
 της παραπάνω εξίσωσης (1), να αποδείξετε ότι κινούνται
της παραπάνω εξίσωσης (1), να αποδείξετε ότι κινούνταιπάνω σε μία υπερβολή.
3. Να βρείτε τον γεωμετρικό τόπο των εικόνων των μιγαδικών
 για τους οποίους ισχύει η σχέση:
για τους οποίους ισχύει η σχέση: .
.4. Να βρεθεί η ελάχιστη απόσταση των εικόνων
 και
και  των μιγαδικών
των μιγαδικών  και
και 
στην περίπτωση κατά την οποία
 .
.Ελπίζω να μην σπατάλησα άδικα τον χρόνο σας.
Σταμ. Γλάρος

 , προκύπτει ο γ.τ.
, προκύπτει ο γ.τ.  .
.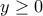 και
και  . Οπότε θεωρώ την συνάρτηση:
. Οπότε θεωρώ την συνάρτηση:  .
. . Επομένως θεωρούμε
. Επομένως θεωρούμε .
.  και
και  .
. η ελάχιστη απόσταση θα πρέπει η ευθεία που διέρχεται από τα σημεία επαφής να είναι κάθετη στις εφαπτομένες. Και προφανώς αυτό δεν ισχύει.
η ελάχιστη απόσταση θα πρέπει η ευθεία που διέρχεται από τα σημεία επαφής να είναι κάθετη στις εφαπτομένες. Και προφανώς αυτό δεν ισχύει. για κάθε
για κάθε  .
. .
. είναι
είναι  . Επομένως το
. Επομένως το  , (όπου
, (όπου  ), ανήκει στην υπερβολή με εξίσωση
), ανήκει στην υπερβολή με εξίσωση  . Μάλιστα είναι σημείο του 1ου τεταρτημορίου αφού
. Μάλιστα είναι σημείο του 1ου τεταρτημορίου αφού  , άρα
, άρα  . Αντίστοιχα το
. Αντίστοιχα το  , με
, με  , ανήκει στην ίδια υπερβολή αλλά στο 4ο τεταρτημόριο.
, ανήκει στην ίδια υπερβολή αλλά στο 4ο τεταρτημόριο. , όπου
, όπου  . Επίσης, παρατηρούμε ότι
. Επίσης, παρατηρούμε ότι  , όπου
, όπου  και
και  .
.
 και επειδή για κάθε σημείο της παραπάνω παραβολής ικανοποιείται η δοθείσα σχέση, ο γεωμετρικός τόπος των εικόνων του
και επειδή για κάθε σημείο της παραπάνω παραβολής ικανοποιείται η δοθείσα σχέση, ο γεωμετρικός τόπος των εικόνων του