 για τον οποίο ισχύουν:
για τον οποίο ισχύουν:
και

Να βρεθεί ο

Συντονιστής: Πρωτοπαπάς Λευτέρης
 για τον οποίο ισχύουν:
για τον οποίο ισχύουν:



 (1)
(1)  ,
,  και
και 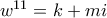 , οπότε η σχέση (1) γράφεται :
, οπότε η σχέση (1) γράφεται :
 και
και 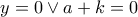 .
. , οπότε
, οπότε  , άτοπο αφού
, άτοπο αφού 
 , τότε
, τότε 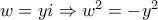 και
και 


 , άτοπο.
, άτοπο.  , τότε
, τότε  και
και  ,
, 
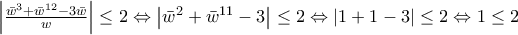 , που ισχύει
, που ισχύει 
 , τότε
, τότε  ,
,  και
και  ,
, 

 , άτοπο.
, άτοπο.  .
. ισοδύναμα έχουμε:
ισοδύναμα έχουμε: \displaystyle{\displaystyle{{{\left| \omega \right|}^{2}}\left( {{{\bar{\omega }}}^{11}}+{{\omega }^{11}} \right)={{\omega }^{2}}{{\bar{\omega }}^{2}}+{{\omega }^{4}}\Leftrightarrow }}
\displaystyle{\displaystyle{{{\left| \omega \right|}^{2}}\left( {{{\bar{\omega }}}^{11}}+{{\omega }^{11}} \right)={{\omega }^{2}}{{\bar{\omega }}^{2}}+{{\omega }^{4}}\Leftrightarrow }}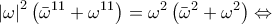
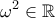 .
. , τότε
, τότε  άρα
άρα  .
. Για
Για  θα είναι
θα είναι  και
και  οπότε όπως ο Θόδωρος καταλήγουμε σε άτοπο.
οπότε όπως ο Θόδωρος καταλήγουμε σε άτοπο. Για
Για  θα είναι
θα είναι 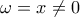 οπότε η (1) γράφεται:
οπότε η (1) γράφεται: , άρα
, άρα  , τιμή η οποία επαληθεύει και την σχέση (2).
, τιμή η οποία επαληθεύει και την σχέση (2).


 Αν
Αν  τότε
τότε
 Αν
Αν  τότε
τότε 

Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες