Έστω οι μιγαδικοί
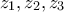 .Αν ισχύουν οι ισότητες
.Αν ισχύουν οι ισότητες 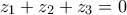 και
και  με p>0, τότε να δείξετε οτι
με p>0, τότε να δείξετε οτι  ,
,
Γνωρίζει κάποιος κάποια λύση (με ύλη Γ Λυκείου);
Συντονιστής: Πρωτοπαπάς Λευτέρης
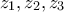 .Αν ισχύουν οι ισότητες
.Αν ισχύουν οι ισότητες 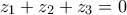 και
και  με p>0, τότε να δείξετε οτι
με p>0, τότε να δείξετε οτι  ,
,
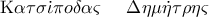
 και λόγω της
και λόγω της 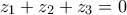 έχουμε
έχουμε 
 από όπου
από όπου  ή
ή 
 μία μη-πραγματική κυβική ρίζα της μονάδας.
μία μη-πραγματική κυβική ρίζα της μονάδας. τότε (αφού
τότε (αφού  )
) 
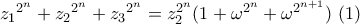
 οπότε η
οπότε η  γίνεται
γίνεται  καθώς
καθώς 
 .
. άρα η ισότητα
άρα η ισότητα  παίρνοντας συζυγείς γίνεται
παίρνοντας συζυγείς γίνεται  άρα
άρα  . Έχουμε
. Έχουμε δηλ.
δηλ.  Η ισότητα
Η ισότητα  γίνεται
γίνεται 
 και όμοια
και όμοια  ,
,  και τελικά
και τελικά  .
. δεν διαιρείται από το 3 ( είναι πρώτος και θα έπρεπε να διαιρεί έναν τουλάχιστον από τους παράγοντες ) οπότε θα είναι της μορφής 3κ+1 ή 3κ+2
δεν διαιρείται από το 3 ( είναι πρώτος και θα έπρεπε να διαιρεί έναν τουλάχιστον από τους παράγοντες ) οπότε θα είναι της μορφής 3κ+1 ή 3κ+2 τότε
τότε 
 τότε
τότε 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 10 επισκέπτες