![\displaystyle{\frac{\prod{(b+c-a)^2}}{8a^2b^2c^2}\leq \frac{\prod{[2a^2-(b-c)^2]}}{(b+c)^2(c+a)^2(a+b)^2}} \displaystyle{\frac{\prod{(b+c-a)^2}}{8a^2b^2c^2}\leq \frac{\prod{[2a^2-(b-c)^2]}}{(b+c)^2(c+a)^2(a+b)^2}}](/forum/ext/geomar/texintegr/latexrender/pictures/17aa941b7027331e1f44efce0fa1babc.png)
Ανισότητα 20
Συντονιστές: vittasko, achilleas, emouroukos
Re: Ανισότητα 20
Αν  ,
,  και
και  , όπου
, όπου 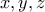 θετικοί πραγματικοί. Η ανισότητα γίνεται
θετικοί πραγματικοί. Η ανισότητα γίνεται

και ισοδύναμα

Θέτω

οπότε έχω ισοδύναμα

ή

Εφόσον
και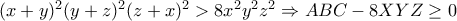
η είναι αληθής αν
είναι αληθής αν 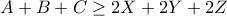
η οποία είναι εύκολα αποδείξιμη
 ,
,  και
και  , όπου
, όπου 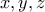 θετικοί πραγματικοί. Η ανισότητα γίνεται
θετικοί πραγματικοί. Η ανισότητα γίνεται 
και ισοδύναμα

Θέτω

οπότε έχω ισοδύναμα

ή

Εφόσον

και
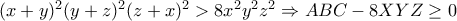
η
 είναι αληθής αν
είναι αληθής αν 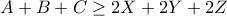
η οποία είναι εύκολα αποδείξιμη
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης
