 και
και  με πλευρές
με πλευρές  και
και  αντίστοιχα. Αν
αντίστοιχα. Αν  είναι η ακτίνα του περιγεγραμμένου κύκλου του
είναι η ακτίνα του περιγεγραμμένου κύκλου του  και
και  η ακτίνα του εγγεγραμμένου κύκλου του
η ακτίνα του εγγεγραμμένου κύκλου του  να αποδειχθεί ότι
να αποδειχθεί ότι 
Συντονιστές: vittasko, achilleas, emouroukos
 και
και  με πλευρές
με πλευρές  και
και  αντίστοιχα. Αν
αντίστοιχα. Αν  είναι η ακτίνα του περιγεγραμμένου κύκλου του
είναι η ακτίνα του περιγεγραμμένου κύκλου του  και
και  η ακτίνα του εγγεγραμμένου κύκλου του
η ακτίνα του εγγεγραμμένου κύκλου του  να αποδειχθεί ότι
να αποδειχθεί ότι 
Επειδή πάει πάλι να ξεχαστεί, βάζω μια λύση:matha έγραψε:Έστωσαν τα τρίγωνακαι
με πλευρές
και
αντίστοιχα. Αν
είναι η ακτίνα του περιγεγραμμένου κύκλου του
και
η ακτίνα του εγγεγραμμένου κύκλου του
να αποδειχθεί ότι
 (1)
(1) (2) (π.χ. είναι
(2) (π.χ. είναι 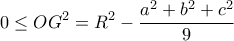 )
) (3)
(3) έχουμε
έχουμε , άρα
, άρα 

Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 10 επισκέπτες