Συνεχίζω με την εξής άσκηση...
Εστω
![\displaystyle{f:\left[ {\alpha ,\beta } \right] \to \left[ {\alpha ,\beta } \right]} \displaystyle{f:\left[ {\alpha ,\beta } \right] \to \left[ {\alpha ,\beta } \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/e2413e1dbc1b5c2b07ed59d0411c0d3c.png) συνάρτηση για την οποία ισχύει:
συνάρτηση για την οποία ισχύει: ,για κάθε
,για κάθε  στο
στο ![\displaystyle{\left[ {\alpha ,\beta } \right]} \displaystyle{\left[ {\alpha ,\beta } \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/732d2d8cc68c4c7a5e1630eb99f15d40.png) .
.Να αποδείξετε οτι
 για κάθε
για κάθε  στο
στο ![\displaystyle{\left[ {\alpha ,\beta } \right]} \displaystyle{\left[ {\alpha ,\beta } \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/732d2d8cc68c4c7a5e1630eb99f15d40.png) .
.Υ.Γ: Επεξεργασία σε latex 22/01/2016
Συντονιστές: m.pαpαgrigorakis, Καρδαμίτσης Σπύρος, Πρωτοπαπάς Λευτέρης, R BORIS, KAKABASBASILEIOS, Μπάμπης Στεργίου
![\displaystyle{f:\left[ {\alpha ,\beta } \right] \to \left[ {\alpha ,\beta } \right]} \displaystyle{f:\left[ {\alpha ,\beta } \right] \to \left[ {\alpha ,\beta } \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/e2413e1dbc1b5c2b07ed59d0411c0d3c.png) συνάρτηση για την οποία ισχύει:
συνάρτηση για την οποία ισχύει: ,για κάθε
,για κάθε  στο
στο ![\displaystyle{\left[ {\alpha ,\beta } \right]} \displaystyle{\left[ {\alpha ,\beta } \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/732d2d8cc68c4c7a5e1630eb99f15d40.png) .
. για κάθε
για κάθε  στο
στο ![\displaystyle{\left[ {\alpha ,\beta } \right]} \displaystyle{\left[ {\alpha ,\beta } \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/732d2d8cc68c4c7a5e1630eb99f15d40.png) .
. στο
στο ![[1,2] [1,2]](/forum/ext/geomar/texintegr/latexrender/pictures/f79408e5ca998cd53faf44af31e6eb45.png) .
.Νίκο, η άσκηση ζητά το σύνολο τιμών να είναι στο [α, β], δηλαδή όπως το πεδίο ορισμού.nsmavrogiannis έγραψε:Χρήστο είναι καλή η εκφώνηση; Φέρνω στο μυαλό μου τηνστο
.
Μαυρογιάννης

![f(x) \in [a,b] f(x) \in [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/267575e79c06cd982d90ba43ba4148b5.png) άρα
άρα
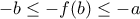 και με πρόσθεση των δύο τελευταίων παίρνουμε
και με πρόσθεση των δύο τελευταίων παίρνουμε 
 . Λόγω των
. Λόγω των  και
και  παίρνουμε
παίρνουμε  .
. και
και ![f(b)=b] f(b)=b]](/forum/ext/geomar/texintegr/latexrender/pictures/2199dc0725ca3cbc66213eaf971a518d.png) ειτε
ειτε  και
και ![f(b)=a] f(b)=a]](/forum/ext/geomar/texintegr/latexrender/pictures/5b42ef373375ddea58efdee724d1e528.png) .
. και
και  : Θέτουμε στην αρχική σχέση
: Θέτουμε στην αρχική σχέση  και παίρνουμε
και παίρνουμε  άρα
άρα  δηλαδή
δηλαδή  , για κάθε
, για κάθε ![x\in[a,b] x\in[a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/c7c42309c359c25dfe77f397d5261997.png) .
. παίρνουμε
παίρνουμε  δηλαδή
δηλαδή  δηλαδή
δηλαδή 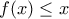 , για κάθε
, για κάθε ![x\in[a,b] x\in[a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/c7c42309c359c25dfe77f397d5261997.png) .
.![\boxed{f(x)=x, \ \ \forall x\in[a,b]} \boxed{f(x)=x, \ \ \forall x\in[a,b]}](/forum/ext/geomar/texintegr/latexrender/pictures/e8015fed3df664a394ea5c88bb66a0b6.png)
 και
και  : Θέτουμε
: Θέτουμε  στην αρχική κι έτσι παίρνουμε
στην αρχική κι έτσι παίρνουμε  δηλαδή
δηλαδή  δηλαδή
δηλαδή 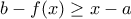 δηλαδή
δηλαδή  για κάθε
για κάθε ![x\in[a,b] x\in[a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/c7c42309c359c25dfe77f397d5261997.png) .
. στην αρχική παίρνουμε
στην αρχική παίρνουμε  δηλαδή
δηλαδή  δηλαδή
δηλαδή 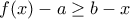 δηλαδή
δηλαδή  , για κάθε
, για κάθε ![x\in[a,b] x\in[a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/c7c42309c359c25dfe77f397d5261997.png) .
. ![\boxed{f(x)=a+b-x, \ \ \forall x\in[a,b]} \boxed{f(x)=a+b-x, \ \ \forall x\in[a,b]}](/forum/ext/geomar/texintegr/latexrender/pictures/5fe0b77373e17348cae3059cdd5853b4.png) .
.....................chris_gatos έγραψε:Εστω f:[α,β]->[α,β] συνάρτηση για την οποία ισχύει:
|f(x)-f(ψ)|>=|χ-ψ|,για κάθε χ,ψ στο [α,β].
Να αποδείξετε οτι |f(x)-f(ψ)|=|χ-ψ| για κάθε χ,ψ στο [α,β]
Βρίσκω καταπληκτικό το αποτέλεσμα που δίνει η απόδειξη του Αλέξανδρου στην πολύ καλή, όπως αποδεικνύεται, έμπνευση της άσκησης.cretanman έγραψε:
....Συνεπώς
....
Ευχαριστώ πολύ για τα καλά σας λόγια κύριε Σερίφη!k-ser έγραψε: Μπράβο και στους δύο: Στον Αλέξανδρο και σ΄αυτόν που εμπνεύστηκε την άσκηση για τον οποίο δεν γνωρίζω κατά πόσο είχε υπόψιν του το αποτέλεσμα που δίνει η απόδειξη του Α. ή, αν φτάνει στο ζητούμενο, χωρίς αυτό!
Μέλη σε αυτήν τη Δ. Συζήτηση: Google [Bot] και 4 επισκέπτες