 είναι παραγωγίσιμη στο διάστημα
είναι παραγωγίσιμη στο διάστημα ![[a, b] [a, b]](/forum/ext/geomar/texintegr/latexrender/pictures/022022f289db140169cd9514f74ee648.png) , και οι παράγωγοι αριθμοί στα δύο άκρα του διαστήματος είναι και οι δύο μεγαλύτεροι (η μικρότεροι) της κλίσης που ορίζεται από τα σημεία
, και οι παράγωγοι αριθμοί στα δύο άκρα του διαστήματος είναι και οι δύο μεγαλύτεροι (η μικρότεροι) της κλίσης που ορίζεται από τα σημεία 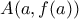 και
και  της
της  , τότε υπάρχει
, τότε υπάρχει 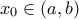 τέτοιο ώστε
τέτοιο ώστε  .
.Συντονιστές: m.pαpαgrigorakis, Καρδαμίτσης Σπύρος, Πρωτοπαπάς Λευτέρης, R BORIS, KAKABASBASILEIOS, Μπάμπης Στεργίου
 είναι παραγωγίσιμη στο διάστημα
είναι παραγωγίσιμη στο διάστημα ![[a, b] [a, b]](/forum/ext/geomar/texintegr/latexrender/pictures/022022f289db140169cd9514f74ee648.png) , και οι παράγωγοι αριθμοί στα δύο άκρα του διαστήματος είναι και οι δύο μεγαλύτεροι (η μικρότεροι) της κλίσης που ορίζεται από τα σημεία
, και οι παράγωγοι αριθμοί στα δύο άκρα του διαστήματος είναι και οι δύο μεγαλύτεροι (η μικρότεροι) της κλίσης που ορίζεται από τα σημεία 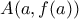 και
και  της
της  , τότε υπάρχει
, τότε υπάρχει 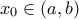 τέτοιο ώστε
τέτοιο ώστε  .
.![g(x)=\left\{\begin{matrix}
f'(a) & & x=a \\
& & \\
\dfrac{f(a)-f(a)}{x-a} & & x \in (a,b]
\end{matrix}\right. g(x)=\left\{\begin{matrix}
f'(a) & & x=a \\
& & \\
\dfrac{f(a)-f(a)}{x-a} & & x \in (a,b]
\end{matrix}\right.](/forum/ext/geomar/texintegr/latexrender/pictures/7691b40931e819a76d52c9d001d3d81c.png)
![[a,b] [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/2c3d331bc98b44e71cb2aae9edadca7e.png) (άρα έχει ελάχιστη τιμή) και παρ/μη στο
(άρα έχει ελάχιστη τιμή) και παρ/μη στο ![(a,b] (a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/a33b8ca44ded30abf82b7dca332e9a96.png) .
. . Αυτό σημαίνει ότι το ελάχιστο της συνάρτησης δεν λαμβάνεται σίγουρα στο
. Αυτό σημαίνει ότι το ελάχιστο της συνάρτησης δεν λαμβάνεται σίγουρα στο  .
. 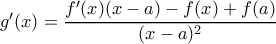 άρα
άρα  από εκφώνηση πάλι.
από εκφώνηση πάλι. ώστε
ώστε  γνησίως αύξουσα άρα
γνησίως αύξουσα άρα  σε αυτό το διάστημα οπότε το ελάχιστο της συνάρτησης δεν λαμβάνεται σίγουρα ούτε στο
σε αυτό το διάστημα οπότε το ελάχιστο της συνάρτησης δεν λαμβάνεται σίγουρα ούτε στο  . Άρα έχουμε ελάχιστο της
. Άρα έχουμε ελάχιστο της  σε κάποιο εσωτερικό σημείο
σε κάποιο εσωτερικό σημείο  του
του  και από Fermat προκύπτει:
και από Fermat προκύπτει: που δίνει τη ζητούμενη.
που δίνει τη ζητούμενη.Καλό.AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ έγραψε: ↑Τετ Απρ 01, 2020 11:10 pmΑν η συνάρτησηείναι παραγωγίσιμη στο διάστημα
, και οι παράγωγοι αριθμοί στα δύο άκρα του διαστήματος είναι και οι δύο μεγαλύτεροι (η μικρότεροι) της κλίσης που ορίζεται από τα σημεία
και
της
, τότε υπάρχει
τέτοιο ώστε
.
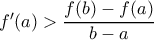 και
και  (όμοια για την ανάποδη ανισότητα). Θέτουμε
(όμοια για την ανάποδη ανισότητα). Θέτουμε
 .
. με
με 
 .
. ανάμεσα στα
ανάμεσα στα  και
και  με
με  . Άρα
. Άρα  , που ισοδυναμεί με το ζητούμενο.
, που ισοδυναμεί με το ζητούμενο. . Με άλλα λόγια η άσκηση του Ανδρέα μας λέει ότι η συνθήκη αυτή στο Θεώρημα Flett είναι περιττή. Με εντυπωσίασε αλλά το παρακάτω ερμηνεύει καλύτερα γιατί αληθεύει η γενίκευση.
. Με άλλα λόγια η άσκηση του Ανδρέα μας λέει ότι η συνθήκη αυτή στο Θεώρημα Flett είναι περιττή. Με εντυπωσίασε αλλά το παρακάτω ερμηνεύει καλύτερα γιατί αληθεύει η γενίκευση.  δεν έχουμε τίποτα να αποδείξουμε, αφού ισχύει το Flett. Ας υποθέσουμε λοιπόν ότι
δεν έχουμε τίποτα να αποδείξουμε, αφού ισχύει το Flett. Ας υποθέσουμε λοιπόν ότι 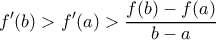 .
. με
με  . Δηλαδή έχουμε
. Δηλαδή έχουμε  . Από Darboux υπάρχει
. Από Darboux υπάρχει  (και άρα
(και άρα  ) με
) με  . Τώρα από το (κανονικό) Flett στο
. Τώρα από το (κανονικό) Flett στο ![[a,q] [a,q]](/forum/ext/geomar/texintegr/latexrender/pictures/92edf7e766e2a4b9cb3067f230a9c5e2.png) υπάρχει
υπάρχει  όπως το ζητάει η άσκηση.
όπως το ζητάει η άσκηση.harrisp έγραψε: ↑Πέμ Απρ 02, 2020 9:38 pmΘεωρούμε τη συνάρτηση:
η οποία είναι συνεχής στο(άρα έχει ελάχιστη τιμή) και παρ/μη στο
.
Από την εκφώνηση.(δεν υπάρχει πρόβλημα αν είναι
) Αυτό σημαίνει ότι το ελάχιστο της συνάρτησης δεν λαμβάνεται σίγουρα στο
. Αυτό σημαίνει ότι αν το ελάχιστο λαμβάνεται στο
τότε θα λαμβάνεται και στο
Ακόμηάρα
από εκφώνηση πάλι.
Άρα από τον ορισμό της παραγώγου υπάρχει διάστημα κοντά στοώστε να ισχύει
σε αυτό το διάστημα οπότε το ελάχιστο της συνάρτησης δεν λαμβάνεται σίγουρα ούτε στο
. Άρα έχουμε ελάχιστο της
σε κάποιο εσωτερικό σημείο
του
και από Fermat προκύπτει:
που δίνει τη ζητούμενη.
Δεν είναι σωστό.Απαιτείται η συνέχεια της παραγώγου.Το ότι
 κοντά στο
κοντά στο  είναι σωστό οπότε δεν χαλάει η απόδειξη.
είναι σωστό οπότε δεν χαλάει η απόδειξη.

Έχετε δίκιο, ευχαριστώ για τη διόρθωση. Στο μυαλό μου σκεφτόμουν τον ορισμό του ορίου και έκανα λογικό άλμα στη λύση με τη μονοτονία για να μη χρειαστεί να γράψω το όριο αλλά την πάτησα.ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Πέμ Απρ 02, 2020 11:08 pmharrisp έγραψε: ↑Πέμ Απρ 02, 2020 9:38 pmΘεωρούμε τη συνάρτηση:
η οποία είναι συνεχής στο(άρα έχει ελάχιστη τιμή) και παρ/μη στο
.
Από την εκφώνηση.(δεν υπάρχει πρόβλημα αν είναι
) Αυτό σημαίνει ότι το ελάχιστο της συνάρτησης δεν λαμβάνεται σίγουρα στο
. Αυτό σημαίνει ότι αν το ελάχιστο λαμβάνεται στο
τότε θα λαμβάνεται και στο
Ακόμηάρα
από εκφώνηση πάλι.
Άρα από τον ορισμό της παραγώγου υπάρχει διάστημα κοντά στοώστε να ισχύει
σε αυτό το διάστημα οπότε το ελάχιστο της συνάρτησης δεν λαμβάνεται σίγουρα ούτε στο
. Άρα έχουμε ελάχιστο της
σε κάποιο εσωτερικό σημείο
του
και από Fermat προκύπτει:
που δίνει τη ζητούμενη.
Δεν είναι σωστό.Απαιτείται η συνέχεια της παραγώγου.Το ότικοντά στο
είναι σωστό οπότε δεν χαλάει η απόδειξη.
Με μπλε το διόρθωσα σε αυτά που έγραψε ο harrisp.
Επίσης μπορούμε να έχουμε στην υπόθεση αντί της
την
Τα πέρασα με μπλε στο κείμενο του harrisp.
![[a,b] [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/2c3d331bc98b44e71cb2aae9edadca7e.png) συνάρτηση
συνάρτηση  έχει θετική παράγωγο στο
έχει θετική παράγωγο στο  η αντίστοιχα αρνητική στο
η αντίστοιχα αρνητική στο  , τότε το αντίστοιχο σημείο είναι θέση τοπικού ελαχίστου (ενώ αν είναι αντίστροφα, είναι θέση μεγίστου). Αυτό προκύπτει άμεσα από τον ορισμό της παραγώγου.
, τότε το αντίστοιχο σημείο είναι θέση τοπικού ελαχίστου (ενώ αν είναι αντίστροφα, είναι θέση μεγίστου). Αυτό προκύπτει άμεσα από τον ορισμό της παραγώγου.![[a,b] [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/2c3d331bc98b44e71cb2aae9edadca7e.png) συνάρτηση
συνάρτηση  έχει στο
έχει στο  παράγωγο μεγαλύτερη από την κλίση της χορδής
παράγωγο μεγαλύτερη από την κλίση της χορδής  τότε υπάρχει σημείο
τότε υπάρχει σημείο  κοντά στο
κοντά στο  που βρίσκεται πάνω από τη χορδή. Όμοια, αν έχει και στο
που βρίσκεται πάνω από τη χορδή. Όμοια, αν έχει και στο  παράγωγο μεγαλύτερη από την κλίση της χορδής, υπάρχει σημείο
παράγωγο μεγαλύτερη από την κλίση της χορδής, υπάρχει σημείο  κοντά στο
κοντά στο  που βρίσκεται κάτω από τη χορδή. Έτσι με θεώρημα
που βρίσκεται κάτω από τη χορδή. Έτσι με θεώρημα  , αποδεικνύεται ότι το γράφημα της συνάρτησης τέμνει τη χορδή τουλάχιστον σε ένα εσωτερικό σημείο του διαστήματός μας.
, αποδεικνύεται ότι το γράφημα της συνάρτησης τέμνει τη χορδή τουλάχιστον σε ένα εσωτερικό σημείο του διαστήματός μας. είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο ![[a,b] [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/2c3d331bc98b44e71cb2aae9edadca7e.png) με
με  και
και  τότε υπάρχει εφαπτομένη της
τότε υπάρχει εφαπτομένη της  που διέρχεται από την αρχή των αξόνων.
που διέρχεται από την αρχή των αξόνων. ![[a,b] [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/2c3d331bc98b44e71cb2aae9edadca7e.png) συνάρτηση, υπάρχει εφαπτομένη της
συνάρτηση, υπάρχει εφαπτομένη της  που διέρχεται από ένα σημείο της ευθείας
που διέρχεται από ένα σημείο της ευθείας  του οποίου η τετμημένη δεν ανήκει στο
του οποίου η τετμημένη δεν ανήκει στο ![[a,b] [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/2c3d331bc98b44e71cb2aae9edadca7e.png) . Προφανώς η παραγωγισιμότητα στα άκρα δεν είναι απαραίτητη (εφαρμογή Θ.
. Προφανώς η παραγωγισιμότητα στα άκρα δεν είναι απαραίτητη (εφαρμογή Θ.  σε κατάλληλη συνάρτηση).
σε κατάλληλη συνάρτηση). σε συνδυασμό των 2 και 3, καθώς και τη γενίκευση που διατύπωσα.
σε συνδυασμό των 2 και 3, καθώς και τη γενίκευση που διατύπωσα. ) που μου επισήμανε ο Σταύρος τον οποίο ευχαριστώ.
) που μου επισήμανε ο Σταύρος τον οποίο ευχαριστώ.Γεια σου Αντρέα.AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ έγραψε: ↑Παρ Απρ 03, 2020 12:33 am3) Αν μία συνάρτησηείναι παραγωγίσιμη στο
με
τότε υπάρχει εφαπτομένη της
που διέρχεται από την αρχή των αξόνων.
.
 είναι τυπογραφικό.
είναι τυπογραφικό.Σταύρο σε ευχαριστώ, το διόρθωσα, Ελπίζω να μην έχω άλλο.ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Παρ Απρ 03, 2020 2:14 pmΓεια σου Αντρέα.AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ έγραψε: ↑Παρ Απρ 03, 2020 12:33 am3) Αν μία συνάρτησηείναι παραγωγίσιμη στο
με
τότε υπάρχει εφαπτομένη της
που διέρχεται από την αρχή των αξόνων.
.
Φυσικά τοείναι τυπογραφικό.
Μήπως υπάρχει και άλλο;
Γεια σου Ανδρέα.AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ έγραψε: ↑Παρ Απρ 03, 2020 9:38 pmΣταύρο σε ευχαριστώ, το διόρθωσα, Ελπίζω να μην έχω άλλο.ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Παρ Απρ 03, 2020 2:14 pmΓεια σου Αντρέα.AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ έγραψε: ↑Παρ Απρ 03, 2020 12:33 am3) Αν μία συνάρτησηείναι παραγωγίσιμη στο
με
τότε υπάρχει εφαπτομένη της
που διέρχεται από την αρχή των αξόνων.
.
Φυσικά τοείναι τυπογραφικό.
Μήπως υπάρχει και άλλο;
Έχεις δίκιο Σταύρο ξέχασα τοΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Παρ Απρ 03, 2020 10:17 pmΓεια σου Ανδρέα.AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ έγραψε: ↑Παρ Απρ 03, 2020 9:38 pmΣταύρο σε ευχαριστώ, το διόρθωσα, Ελπίζω να μην έχω άλλο.ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Παρ Απρ 03, 2020 2:14 pmΓεια σου Αντρέα.AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ έγραψε: ↑Παρ Απρ 03, 2020 12:33 am3) Αν μία συνάρτησηείναι παραγωγίσιμη στο
με
τότε υπάρχει εφαπτομένη της
που διέρχεται από την αρχή των αξόνων.
.
Φυσικά τοείναι τυπογραφικό.
Μήπως υπάρχει και άλλο;
Με μόνο αυτές τις προυποθέσεις δεν ισχύει.
Δεν νομίζω ότι χρειάζεται να βάλω παράδειγμα.
Υποθέτω ότι έχεις και άλλες προυποθέσεις που τις ξέχασες.

Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες