Έστω
 συνεχής.
συνεχής.α)Αν
 να δείξετε ότι η f δεν είναι 1-1.
να δείξετε ότι η f δεν είναι 1-1.β) Αν
 να δείξετε ότι υπάρχουν
να δείξετε ότι υπάρχουν ![a,b\epsilon[2,8] a,b\epsilon[2,8]](/forum/ext/geomar/texintegr/latexrender/pictures/1b078c75a646810d8ed346ba5eef2c5e.png) με
με  ώστε
ώστε  .
.Θα ήθελα κάποια βοήθεια γιατί είμαι σε αδιέξοδο.(Τα δύο ερωτήματα είναι ανεξάρτητα μεταξύ τους.)Ευχαριστώ.
Συντονιστές: m.pαpαgrigorakis, Καρδαμίτσης Σπύρος, Πρωτοπαπάς Λευτέρης, R BORIS, KAKABASBASILEIOS, Μπάμπης Στεργίου
 συνεχής.
συνεχής. να δείξετε ότι η f δεν είναι 1-1.
να δείξετε ότι η f δεν είναι 1-1. να δείξετε ότι υπάρχουν
να δείξετε ότι υπάρχουν ![a,b\epsilon[2,8] a,b\epsilon[2,8]](/forum/ext/geomar/texintegr/latexrender/pictures/1b078c75a646810d8ed346ba5eef2c5e.png) με
με  ώστε
ώστε  .
.α) Αν ο μικρότερος τωνpanagiotis iliopoulos έγραψε: ↑Κυρ Σεπ 22, 2019 6:06 pmΚαλησπέρα σας. Προσπάθησα να λύσω από ένα παλιό περιοδικό του Ευκλείδη το εξής θέμα:
Έστωσυνεχής.
α)Αννα δείξετε ότι η f δεν είναι 1-1.
β) Αννα δείξετε ότι υπάρχουν
με
ώστε
.
Θα ήθελα κάποια βοήθεια γιατί είμαι σε αδιέξοδο.(Τα δύο ερωτήματα είναι ανεξάρτητα μεταξύ τους.)Ευχαριστώ.
 είναι μικρότερο τους
είναι μικρότερο τους  τότε ο άλλος είναι μεγαλύτερος (ή ίσος οπότε τελειώσαμε) και άρα από θεώρημα ενδιάμεσων τιμών υπάρχει
τότε ο άλλος είναι μεγαλύτερος (ή ίσος οπότε τελειώσαμε) και άρα από θεώρημα ενδιάμεσων τιμών υπάρχει  με
με 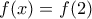 . Το ίδιο ισχύει και για το
. Το ίδιο ισχύει και για το  (με μεγαλύτερο αντι για μικρότερο) άρα υποθέτουμε ότι
(με μεγαλύτερο αντι για μικρότερο) άρα υποθέτουμε ότι  . Έχουμε δύο περιπτώσεις
. Έχουμε δύο περιπτώσεις  τελειώσαμε.
τελειώσαμε.  ή
ή  που τελειώνουν με θεώρημα ενδιάμεσων τιμών στο
που τελειώνουν με θεώρημα ενδιάμεσων τιμών στο 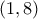 και
και  αντίστοιχα.
αντίστοιχα.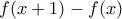 . Αυτή διατηρεί σταθερό πρόσημο. Όμως αθροίζοντας
. Αυτή διατηρεί σταθερό πρόσημο. Όμως αθροίζοντας  ,
,  ,
,  ,
,  ,
,  ,
,  και
και  παίρνουμε ότι το
παίρνουμε ότι το  έχει το πρόσημο της
έχει το πρόσημο της 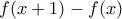 άτοπο. Άρα ισχύει έμμεσα το ζητούμενο.
άτοπο. Άρα ισχύει έμμεσα το ζητούμενο. .Εφαρμόζουμε το Θ.Ε.Τ στο διάστημα
.Εφαρμόζουμε το Θ.Ε.Τ στο διάστημα ![[2,8] [2,8]](/forum/ext/geomar/texintegr/latexrender/pictures/60fe7d62d10c721e8bc3c5e121a4f922.png) οπότε
οπότε ωστε
ωστε  .
.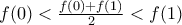 ή
ή 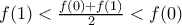 (*)
(*)![[0,1] [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png) υπάρχει
υπάρχει  ωστε
ωστε  .
. και
και  .
. δεν είναι
δεν είναι  .
. τότε πάλι η
τότε πάλι η  δεν είναι
δεν είναι 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες