οι παραγωγίσιμες συναρτήσεις
 στο
στο  ,
,  ,
, .
.Να λυθεί το σύστημα:
 .
.Συντονιστής: Πρωτοπαπάς Λευτέρης
 στο
στο  ,
,  ,
, .
. .
. λύση του συστήματος
λύση του συστήματος  . Μετά από πράξεις,
. Μετά από πράξεις, . Από την τελευταία,
. Από την τελευταία, .
. ή ισοδύναμα
ή ισοδύναμα
![\displaystyle{p(k)=k^3+6\,k^2+11\,k+6\in\mathbb{R}[x]} \displaystyle{p(k)=k^3+6\,k^2+11\,k+6\in\mathbb{R}[x]}](/forum/ext/geomar/texintegr/latexrender/pictures/6e1942abfe69eacba2064932b9f93397.png) , το οποίο γράφεται ώς
, το οποίο γράφεται ώς 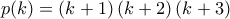 με ρίζες
με ρίζες 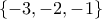 . Τελικά,
. Τελικά, και άρα με αντικαταστάση
και άρα με αντικαταστάση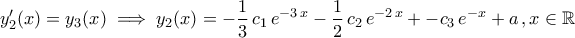
 .
. είναι απλή και βολεύει και αυτό που έκανε ο Ευάγγελος.
είναι απλή και βολεύει και αυτό που έκανε ο Ευάγγελος. , που είναι οι ιδιοτιμές του πίνακα
, που είναι οι ιδιοτιμές του πίνακα  .
. έχουμε ότι το αντίστοιχο ιδιοδιάνυσμα είναι
έχουμε ότι το αντίστοιχο ιδιοδιάνυσμα είναι  .
. έχουμε ότι το αντίστοιχο ιδιοδιάνυσμα είναι
έχουμε ότι το αντίστοιχο ιδιοδιάνυσμα είναι  .
. έχουμε ότι το αντίστοιχο ιδιοδιάνυσμα είναι
έχουμε ότι το αντίστοιχο ιδιοδιάνυσμα είναι  .
. ,
, , όπου
, όπου  .
. .
.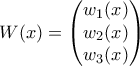 , από την
, από την  βρίσκουμε ότι:
βρίσκουμε ότι:
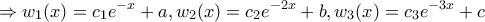 .
.

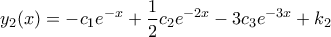
 .
. .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 8 επισκέπτες